Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b:
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
c: góc OBC=góc HBD
góc OCB=góc KCE
mà góc HBD=góc KCE
nên góc OBC=góc OCB
=>ΔOBC cân tại O

A B C D E H K
a) Vì \(\Delta ABC\) cân tại A
=> \(\widehat{B}=\widehat{C}\)
mà \(\widehat{ABD}+\widehat{ABC}=180^0\) (kề bù)
và \(\widehat{ACB}+\widehat{ACE}=180^0\) (kề bù)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét \(\Delta ABC\) và \(\Delta ACE\) có:
AB = AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
DB = CE (gt)
Do đó: \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
=> \(\widehat{D}=\widehat{E}\) ( hai góc tương ứng)
Xét \(\Delta DBH\) và \(\Delta ECK\) có:
\(\widehat{DHB}=\widehat{CKE}\) ( = 900)
DB = CE (gt)
\(\widehat{D}=\widehat{E}\)(cmt)
Do đó: \(\Delta DBH=\Delta ECK\) (ch -gn)
=> BH = CK (hai cạnh tương ứng)
b) Xét \(\Delta ABH\) và \(\Delta ACK\) có:
CK = BH ( cmt )
\(\widehat{AHB}=\widehat{AKC}\left(=90^0\right)\)
AB = AC (gt)
Do đó: \(\Delta ABH=\Delta ACK\) ( cạnh huyền - cạnh góc vuông)
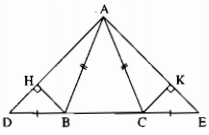
a) Vì ∆ABC cân tại A nên góc ABC =góc ACB (tính chất tam giác cân)
Ta có: góc ABC + góc ABD=180o (hai góc kề bù)
góc ACB + góc ACE=180o (hai góc kề bù)
Suy ra: góc ABD = góc ACE
Xét ∆ABD và ∆ACE, ta có:
AB = AC (gt)
góc ABD = góc ACE (chứng minh trên)
BD = CE (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
⇒ góc D = góc E (hai góc tương ứng)
Xét hai tam giác vuông BHD và CKE, ta có:
góc BHD =góc CKE=90o
BD = CE (gt)
góc D = gócE (chứng minh trên)
Suy ra: ∆BHD = ∆CKE (cạnh huyền, góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Xét tam giác vuông AHB và ACK, ta có:
góc AHB = gócAKC = 90o
AB = AC (gt)
BH = CK (chứng minh trên)
Suy ra: ∆ABH = ∆ACK (cạnh huyền, cạnh góc vuông)

B B C C A A D D E E H H K K
a) Do tam giác ABC cân tại A nên \(AB=AC;\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{ABD}=\widehat{ACE}\)
Vậy thì \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
b) Do \(\Delta ABD=\Delta ACE\Rightarrow\widehat{KDC}=\widehat{HEB}\)
Lại có DC = DB + BC = CE + BC = BE
Vậy thì \(\Delta DKC=\Delta EHB\) (Cạnh huyền góc nhọn)
\(\Rightarrow BH=CK\)
c) Xét hai tam giác vuông ABH và ACK có :
BH = CK
AC = AC
\(\Rightarrow\Delta BAH=\Delta CAK\) (Cạnh huyền - cạnh góc vuông)

Hình tự vẽ nha
a) Vì tam giác ABC cân tại A
=> ABC = ACB (1)
Ta có ABC + ABD = ACB + ACE ( cùng = 1800 ) (2)
Từ (1) và (2) => ABD = ACE
Xét tam giác ABD và tam giác ACE có :
AB = AC ( gt )
ABD = ACE ( cmt )
BD = CE ( gt )
=> tam giác ABD = tam giác ACE ( c-g-c )
=> D = E
Xét tam giác BHD và tam giác CKE có :
DHB = EKC ( = 900 )
BD = CE ( gt )
D = E ( cmt )
=> tam giác BHD = tam giác CKE ( ch - gn )
=> đpcm
b) Vì tam giác ABD = tam giác ACE ( chứng minh câu a )
=> HAB = KAC ( 2 góc tương ứng )
Xét tam giác AHB và tam giác AKC có :
HAB = KAC ( cmt )
AHB = AKC ( = 900 )
AB = AC ( gt )
=> tam giác AHB = tam giác AKC ( ch - gn )
=> đpcm
c) Nối H với K
Xét tam giác ADE cân tại A ( vì AD = AE )
=> \(\widehat{D}=\frac{180^0-\widehat{DAE}}{2}\left(1\right)\)
Xét tam giác AHK cân tại A ( vì AH = AK )
\(\Rightarrow\widehat{AHK}=\frac{180^0-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) => D = AHK
mà 1 góc này ở vị trí đồng vị
=> HK // DE hay HK // BC ( đpcm )
Có j lên đây hỏi nha : Group Toán Học

1
a) trước tiên chứng minh\(\widehat{ABM}=\widehat{ACN}\)
rồi mới chứng minh 2 tam giác ABM và ACN bằng nhau
suy ra AM = AN
b)Đầu tiên chứng minh\(\widehat{ABH}=\widehat{ACK}\)
rồi chứng minh hai tam giác ABH và ACK bằng nhau
suy ra BH = CK
c) vì hai tam giác ABH và ACK bằng nhau (cmt)
nên AH = AK
d) ta có \(\widehat{AMB}=\widehat{ACN}\)(hai tam giác ABH và ACK bằng nhau)
nên dễ cm \(\widehat{MBH}=\widehat{NCK}\)
còn lại tự cm
e) dễ cm tam giác ABC đều
vẽ \(BH\perp AC\)
nên BH vừa là đường cao; phân giác và trung tuyến
dễ cm \(\Delta BHC=\Delta NKC\)
nên \(\widehat{BCH}=\widehat{NCK}=60^0\)
từ đó dễ cm AMN cân và OBC dều
a) Tam giác ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow180^0-\widehat{ABC}=180^0-\widehat{ACB}\)
Hay \(\widehat{ABD}=\widehat{ACE}\)
Theo định lý Cos ta có
\(AD=\sqrt{DB^2+AB^2-2\cdot DB\cdot AB\cdot\cos DBA}\)
\(AE=\sqrt{AC^2+CE^2-2\cdot AC\cdot CE\cdot\cos ACE}\)
Vì AB = AC ( tam giác ABC cân tại A ) và DB =CE và góc DBA = góc ACE
Nên AD = AE hay tam giác ADE cân tại A
b)\(\widehat{ADB}=\widehat{AEC}\)(ADE cân)
Nên góc KCE = góc DBH
Vậy \(\widehat{HBA}=\widehat{KCA}\)( góc DBA = góc ACE)
Xét tam giác HBA và tam giác ACK vuông có :
+ góc HBA = góc KCA
+ AB = AC
\(\Rightarrow\Delta HBA=\Delta KCA\left(ch-gn\right)\)=> HB = KC (hai cạnh tương ứng)
c) Ta có \(180^0=\widehat{HBA}+\widehat{ABC}+\widehat{OBC}\)
\(180^0=\widehat{ACK}+\widehat{ACB+\widehat{OCB}}\)
\(\widehat{HBA}=\widehat{ACK}\)
\(\widehat{ABC}=\widehat{ACB}\)
Nên \(\widehat{OCB}=\widehat{OBC}\)hay tam giâc OBC cân tại O
d) Xét tam giác AMB và tam giác AMC
+ AM chung
+ BM = MC (gt)
+ AB = AC (gt)
Vậy hai tam giác trên bằng nhau theo trường hợp c-c-c
Và hai góc BAM = góc CAM
Hay AM là tia phân giác của góc BAC
Xét tam giác AOB và tam giác ACO
+ AB = AC (gt)
+ OB = OC (cmt )
+ góc ABO = góc ACO vì \(\widehat{ABM+\widehat{OBC}=\widehat{ACM}+\widehat{OCB}}\)
Vậy hai tam giác trên bằng nhau theo trường hợp c-g-c
Và góc BAO = góc CAO
Hay AO là phân giác của góc BAC
Một góc chỉ có duy nhất một tia phân giác nên AM và AO là một hay A,M,O thẳng hàng