DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
2
6 tháng 4 2022
ta có:\(sin\alpha.cosb=\dfrac{1}{2}\left[sin\left(a-b\right)+sin\left(a+b\right)\right]\)
\(=\dfrac{1}{2}\left[\dfrac{2}{5}+\left(-\dfrac{3}{5}\right)\right]\)
\(=\dfrac{1}{2}.\left(-\dfrac{1}{5}\right)\)
\(=-\dfrac{1}{10}\)
MH
6 tháng 4 2022
Ta có \(sin\left(a-b\right)+sin\left(a+b\right)=2sin\left(\dfrac{a-b+a+b}{2}\right)cos\left(\dfrac{a+b-\left(a-b\right)}{2}\right)\\ \Rightarrow2sin\left(a\right).cos\left(b\right)=\dfrac{2}{5}+\left(-\dfrac{3}{5}\right)=-\dfrac{1}{5}\\ \Rightarrow sin\left(a\right)cos\left(b\right)=-\dfrac{1}{10}\)
23 tháng 3 2018
rút gọn biểu thức:
E=cos(\(\dfrac{3\pi}{3}-\alpha\))-sin(\(\dfrac{3\pi}{2}-\alpha\))+sin(\(\alpha+4\pi\))
TH
1
26 tháng 3 2022
Tham khảo
sin(a+b) = sina.cosb + cosa.sinb = 1, suy ra cosa.sinb = 1 - sina.cosb.
sin(a-b) = sina.cosb - cosa.sinb = sina.cosb - (1 - sina.cosb) = 2sina.cosb - 1=1/2.
Vậy sina.cosb=(1/2+1):2=3/4.
17 tháng 4 2017
a) \(\dfrac{\sin2\text{a}+\cos a}{1+\cos2\text{a}+\cos a}=2\tan a\)
BT
9 tháng 5 2017
a) \(\dfrac{sin2\alpha+sin\alpha}{1+cos2\alpha+cos\alpha}=\dfrac{2sin\alpha cos\alpha+sin\alpha}{2cos^2\alpha+cos\alpha}\)\(=\dfrac{sin\alpha\left(2cos\alpha+1\right)}{cos\alpha\left(2cos\alpha+1\right)}=\dfrac{sin\alpha}{cos\alpha}=tan\alpha\).
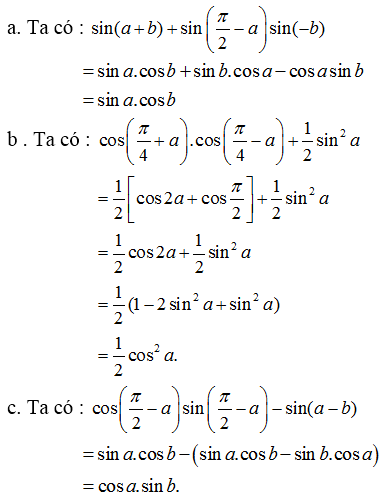
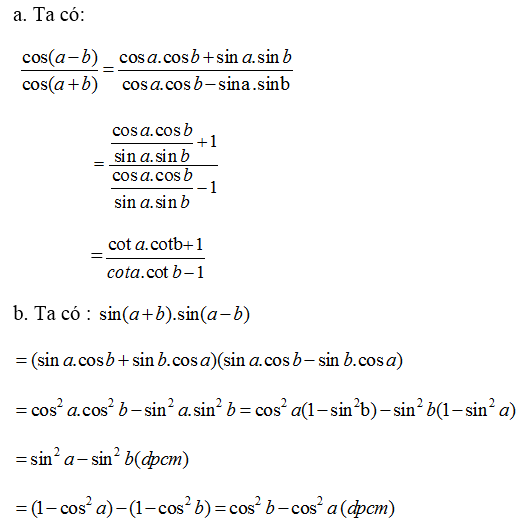
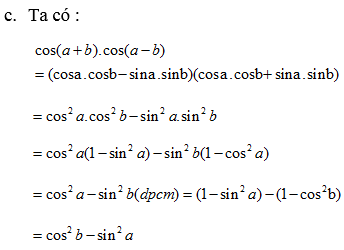
sin(a+b) = sina.cosb + cosa.sinb = 1, suy ra cosa.sinb = 1 - sina.cosb.
sin(a-b) = sina.cosb - cosa.sinb = sina.cosb - (1 - sina.cosb) = 2sina.cosb - 1=1/2.
Vậy sina.cosb=(1/2+1):2=3/4.