Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3.
Tính số học sinh của lớp 6A.
lớp của 6A trường câụ là bao nhiêu rồi ghi vó là được
chúc bạn học tốt

\(=11\cdot\left(\frac{5}{11.16}+\frac{5}{16.21}+...+\frac{5}{36.41}\right)\)
\(=11\cdot\left(\frac{1}{11}-\frac{1}{16}+\frac{1}{16}-\frac{1}{21}+...+\frac{1}{36}-\frac{1}{41}\right)\)
\(=11\cdot\left(\frac{1}{11}-\frac{1}{41}\right)\)
\(=11\cdot\frac{30}{451}\)
\(=\frac{30}{41}\)


Gọi d là ƯCLN(2n+5,n+3)(d\(\in\)N*)
Ta có:\(2n+5⋮d,n+3⋮d\)
\(\Rightarrow2n+5⋮d,2\cdot\left(n+3\right)⋮d\)
\(\Rightarrow2n+5⋮d,2n+6⋮d\)
\(\Rightarrow\left(2n+6\right)-\left(2n+5\right)⋮d\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
Vì ƯCLN(2n+5,n+3)=1
\(\Rightarrow\frac{2n+5}{n+3}\) là phân số tối giản
Gọi d là ƯCLN(2n+5,n+3)(d∈
N*)
Ta có:2n+5⋮d,n+3⋮d
⇒2n+5⋮d,2⋅(n+3)⋮d
⇒2n+5⋮d,2n+6⋮d
⇒(2n+6)−(2n+5)⋮d
⇒1⋮d⇒d=1
Vì ƯCLN(2n+5,n+3)=1

Câu 10 :
\(x+3,5=6,72+3,28\)
\(\Rightarrow x+3,5=10\)
\(\Rightarrow x=6,5\)
\(x+3,5=6,72+3,28\)
\(\Rightarrow x+3,5=10\)
\(\Rightarrow x=10-3,5\)
\(\Rightarrow x=6,5\)
~ Hok tốt ~

a) \(x-\frac{1}{2}=\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{19.20}\)
\(x-\frac{1}{2}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{19}-\frac{1}{20}\)
\(x-\frac{1}{2}=1-\frac{1}{20}=\frac{19}{20}\)
\(x=\frac{19}{20}+\frac{1}{2}=\frac{29}{20}\)
b) (x + 1) + (x + 2) + (x + 3) + ... + (x + 100) = 5750
(x + x + x + ... + x) + (1 + 2 + 3 + ... + 100) = 5750 (100 số x)
(100x) + 5050 = 5750
100x = 700
x = 7.


a,Ta có \(\dfrac{1}{2.3}\)=\(\dfrac{1}{6}\)
\(\dfrac{1}{2}-\dfrac{1}{3}\)=\(\dfrac{3}{6}-\dfrac{2}{6}\)=\(\dfrac{1}{6}\)
=>\(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
b, \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2005.2006}\)
=\(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+....+\dfrac{1}{2005}-\dfrac{1}{2006}\)
=\(\dfrac{1}{1}-\dfrac{1}{2006}\)
=\(\dfrac{2006}{2006}-\dfrac{1}{2006}\)
=\(\dfrac{2005}{2006}\)
Ta có
\(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{\left(n+1\right)-n}{n.\left(n+1\right)}=\dfrac{1}{n.\left(n+1\right)}\)
Vậy \(\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
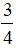 . Nếu cộng thêm 12 vào tử số thì cần phải cộng thêm số nào vào mẫu số để được phân số mới vẫn bằng
. Nếu cộng thêm 12 vào tử số thì cần phải cộng thêm số nào vào mẫu số để được phân số mới vẫn bằng 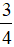 ?
?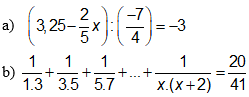
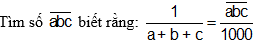







A
Chọn A