Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc BFC=góc BEC=90 độ
=>BCEF nội tiếp
b: Xét ΔKFB và ΔKCE có
góc KFB=góc KCE
góc K chung
=>ΔKFB đồng dạng với ΔKCE
=>KF/KC=KB/KE
=>KF*KE=KB*KC

từ điểm O nằm ngoài đương tròn vẽ hai tiếp tuyến AB và AC vẽ dây BD song song AC AD cắt tại K tia BK cắt AC tại I
chứng minh IC bình =IK.IB
tam giácBAI đồng dạng tam giác AKI
i là trung điểm ac
tìm vị trí A để CK vuông góc AB

Do tứ giác BCEF nội tiếp nên ME . MF = MB . MC
Lại có tứ giác BCKA nội tiếp nên MC . MB = MK . MA
Suy ra MK . MA = ME . MF nên tứ giác AKEF nội tiếp.
Mà tứ giác AEHF nội tiếp nên 5 điểm A, E, F, H, K đồng viên.
Suy ra \(\widehat{HKA}=\widehat{HEA}=90^o\Rightarrow HK\perp AM\).

a) Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^o+90^o=180^o\)
=> AEHF là tứ giác nt
b) Xét tứ giác BCEF có 2 góc \(\widehat{BFC}\)và \(\widehat{CEB}\)cùng nhìn đoạn BC một góc 90o
=> BCEF là tứ giác nt
=> \(\widehat{KBF}=\widehat{KEC}\)(cùng bù với \(\widehat{FBC}\))
Xét \(\Delta KBF\)và \(\Delta KEC\)có
\(\widehat{KBF}=\widehat{KEC}\)
\(\widehat{CKE}\)chung
=> \(\Delta KBF\)ᔕ \(\Delta KEC\)(g-g)
=> \(\frac{KB}{KE}=\frac{KF}{KC}\)
=> KB . KC = KE . KF (1)
c) Nối M với B
Xét (O) có tứ giác AMBC nội tiếp đường tròn đó
=> \(\widehat{KBM}=\widehat{KAB}\)
Xét \(\Delta KBM\)và \(\Delta KAC\)có
\(\widehat{KBM}=\widehat{KAC}\)
\(\widehat{AKC}\)chung
=> \(\Delta KBM\)ᔕ \(\Delta KAC\)(g.g)
=> \(\frac{KB}{KA}=\frac{KM}{KC}\)=> KB . KC = KA . KM (2)
Từ (1) (2) => KE . KF = KA . KM
=> \(\frac{KF}{KA}=\frac{KM}{KE}\)
Xét \(\Delta KFMvà\Delta KAE\)có
\(\widehat{AFE}\)chung
\(\frac{KF}{KA}=\frac{KM}{KE}\)
=> \(\Delta KFM\)ᔕ \(\Delta KAE\)(g-g) <=> \(\widehat{KMF}=\widehat{KEA}\)hay \(\widehat{KMF}=\widehat{FEA}\)
Xét tứ giác AMFE có \(\widehat{KMF}=\widehat{FEA}\)=> AMFE là tứ giác nội tiếp
=> A, M, F ,E cùng thuộc một đường tròn
Mà A, F, H,E cùng thuộc một đường tròn (AFHE là tgnt)
=> A,F,M,H,E cùng thuộc một đường tròn
=> AMHE là tứ giác nt
=> \(\widehat{AMH}+\widehat{AEH}=180^o\)=> \(\widehat{AMH}=180^o-\widehat{AEH}=180^o-90^o=90^o\)
=> \(MH\perp AK\)
PHẦN D NGHĨ SAU NHÉ
d) À mik có ghi thiếu. Câu d c/m: MH cố định khi A di chuyển trên cung lớn BC

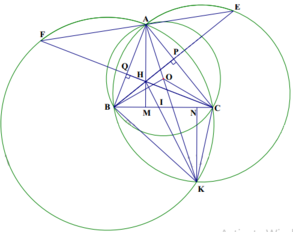
a, Ta có AKB =AEB (vì cùng chắn cung AB của đường tròn ngoại tiếp tam giác AEB)
Mà ABE =AEB (tính chất đối ứng) suy ra AKB= ABE (1)
AKC= AFC (vì cùng chắn cung AC của đường tròn ngoại tiếp tam giác AFC)
ACF= AFC (tính chất đối x
Bài giảng học thử
Video không hỗ trỡ trên thiết bị của bạn!
Bài 8. Bài toán hai tiếp tuyến cắt nhau - Phần 2 - Tổng ôn Toán vào 10 - Cô Nguyễn Hồng Nhung
Video không hỗ trỡ trên thiết bị của bạn!
Bài 1. Đại cương về hệ phương trình bậc nhất 2 ẩn - Phần 3 - Tổng ôn Toán vào 10 - Cô Nguyễn Hồng Nhung
Video không hỗ trỡ trên thiết bị của bạn!
Bài 6. Ôn tập chương Phần 3 - Toán 9 - Thầy Trần Trung Hải
Video không hỗ trỡ trên thiết bị của bạn!
Dạng 1: Toán chuyển động - Phần 3. Chuyển động ngược xuôi trên sông - TỔNG ÔN Toán 9 - Cô Vương Thị Hạnh
Video không hỗ trỡ trên thiết bị của bạn!
Bài học 2: Đề số 3 (Phần 2) - LUYỆN ĐỀ ôn thi vào 10 - Cô Vương Thị Hạnh

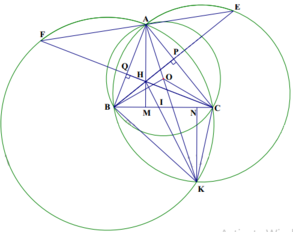
Gọi (O’) là đường tròn đi qua bốn điểm B, H,C, K. Ta có dây cung B C = R 3
BKC=60o= BAC nên bán kính đường tròn (O’) bằng bán kính R của đường tròn (O).
Gọi M là giao điểm của AH và BC thì MH vuông góc với BC, kẻ KN vuông góc với BC (N thuộc BC), gọi I là giao điểm của HK và BC.
Bài giảng học thử
Video không hỗ trỡ trên thiết bị của bạn!
Bài 8. Bài toán hai tiếp tuyến cắt nhau - Phần 2 - Tổng ôn Toán vào 10 - Cô Nguyễn Hồng Nhung
Video không hỗ trỡ trên thiết bị của bạn!
Bài 1. Đại cương về hệ phương trình bậc nhất 2 ẩn - Phần 3 - Tổng ôn Toán vào 10 - Cô Nguyễn Hồng Nhung
Video không hỗ trỡ trên thiết bị của bạn!
Bài 6. Ôn tập chương Phần 3 - Toán 9 - Thầy Trần Trung Hải
Video không hỗ trỡ trên thiết bị của bạn!
Dạng 1: Toán chuyển động - Phần 3. Chuyển động ngược xuôi trên sông - TỔNG ÔN Toán 9 - Cô Vương Thị Hạnh
Video không hỗ trỡ trên thiết bị của bạn!
Bài học 2: Đề số 3 (Phần 2) - LUYỆN ĐỀ ôn thi vào 10 - Cô Vương Thị Hạnh