Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

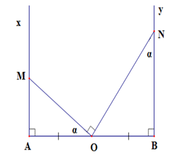
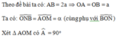
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
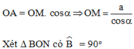
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
![]()
Vậy diện tích tam giác MON là:
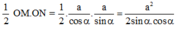
Đáp án cần chọn là: A

a: Xét (O) có
OM là bán kính
EF vuông góc OM tại M
Do đó: EF là tiếp tuyến của (O)
b: Xét (O) có
EM.EA là tiếp tuyến
nên EM=EA
Xét(O) có
FM,FB là tiếp tuyến
nên FM=FB
EF=EM+MF
=>EF=EA+FB

a: Xét (O) có
OM là bán kính
EF\(\perp\)OM tại M
Do đó: EF là tiếp tuyến của (O)
b: Xét (O) có
EM,EA là các tiếp tuyến
Do đó: EM=EA
Xét (O) có
FM,FB là các tiếp tuyến
Do đó: FM=FB
Ta có: EF=EM+MF
mà EM=EA và FM=FB
nên EF=EA+FB

Cho o là trung điểm của đoạn AB. Trên cùng môtj nửa mặt phẳng có bờ là cạnh AB vẽ tia Ax, By cùng vuông góc với Ab. TRên tia Ax lấy C( khác A), qua o kẻ đường thawnggr vuông góc với OC cắt By tại D.
a. CM: (AB)^2= 4AC.BD

minh se noi cach tu duy cua minh, mong ban hieu
AB^2=4AC.BD=>(2OA)^2=4AC.BD=>4OA^2=4AC.BD=>Ban phai chung minh OA^2=AC.BD
Day la cach chung minh: goc COA+COD+DOB=180
Ma COD=90(theo gt)=>COA+BOD=90(1)
Trong tam giac COA co CAO=90:COA+ACO=90(2)
Tu (1)va(2) ta=>BOD=ACO
xet tam giac CAO va OBD co:
CAO=OBD=90
BOD=ACO(theo cm tren)
=>tam giac CAO dong dang voi tam giac OBD=>AC/OA=OB/BD=>AC/OA=OA/BD=>OA^2=AC.BD