Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C D H M O K
Kéo dài HO về phía O cắt (o) tại K => KH là đường kính (o). Nối CH; CK ta có
^KCH=90 (góc nội tiếp chắn nửa đường tròn)
CM=DM=CD/2=8 cm (bán kính vuông góc với dây cung thì chia đôi dây cung)
Xét tg vuông KCH có \(CM^2=MH.MK\Rightarrow8^2=4.MK\Rightarrow MK=16cm\)
\(\Rightarrow KH=MH+MK=4+16=20cm\Rightarrow OK=\frac{KH}{2}=10cm\)

Đặt OH = x cm (R = OH)
Ta có OM = x – 4 cm
Áp đụng định lý Pytago ta tìm được x = 10cm

Gọi MP, QP cắt AB tại K, L
Ta chứng minh được PQ vuông góc AB
\(\Delta\)AON đồng dạng \(\Delta\)APB suy ra \(AN=AM=\sqrt{OA^2+OM^2}=\frac{R\sqrt{5}}{2}\)
\(\frac{AO}{AP}=\frac{ON}{PB}=\frac{AN}{AB}\Rightarrow\frac{R}{AP}=\frac{\frac{R}{2}}{PB}+\frac{\frac{R\sqrt{5}}{2}}{2R}=\frac{\sqrt{5}}{4}\Rightarrow AP=\frac{4R\sqrt{5}}{5};BP=\frac{2R\sqrt{5}}{5}\)
Ta có
\(BP^2=BL.AB\Rightarrow BL=\frac{BP^2}{AB}=\frac{2R}{5};OL=OB-BL=\frac{3R}{5};PL=\sqrt{BP^2-BL^2}=\frac{4R}{5}\)\(\frac{KL}{OK}=\frac{KP}{MK}=\frac{PL}{OM}=\frac{\frac{4R}{5}}{\frac{R}{2}}=\frac{8}{5}\Rightarrow\frac{KL}{8}=\frac{OK}{5}=\frac{OL}{13}=\frac{\frac{3R}{5}}{13}=\frac{3R}{65}\Rightarrow KL=\frac{24R}{65};OK=\frac{3R}{13}\)
\(MP=MK+KP=\sqrt{OM^2+OK^2}+\sqrt{KL^2+PL^2}=\frac{\sqrt{205}R}{10}\)
có \(MP=\frac{\sqrt{205}R}{10},AP=\frac{4R\sqrt{5}}{5};AM=\frac{R\sqrt{5}}{2}\)
\(AM^2+MP^2\ne AP^2\)nên MA không vuông góc MP
Sorry, vừa rồi mình nhầm O với giao điểm của AB với QN.
Mình sửa lại như sau: Gọi H là giao của QN và AB, F là giao của AB và QP. Từ P vẽ PK vuông góc với CD tại K.
Giả sử AQ vuông góc với MP suy ra H là trực tâm tam giác AQP. Suy ra BH = 2 . BF.
Vì HN song song với BP và PK // AO ta có đẳng thức sau:
NK/NO = PK / AO = NP/NA = BH/HA
suy ra
(r-KD)/(r/2) = (r-BF)/r = 2BF/(2r-2BF)
ở đó r là bán kính đường tròn (O). Ngoài ra ta còn có BF.(2r-BF) = PF^2 = (r-KD)^2
Từ đó rút ra điều vô lý.
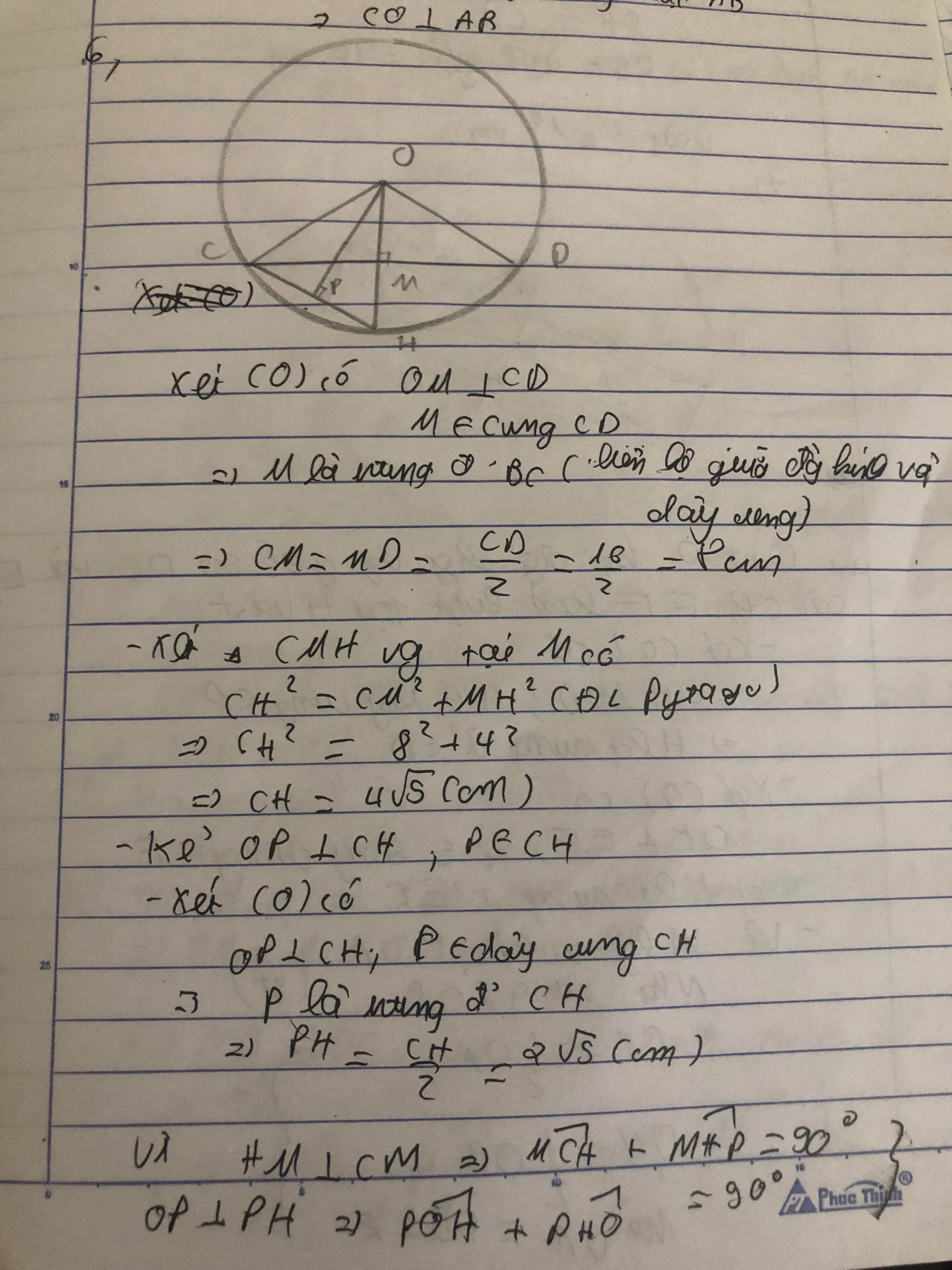

Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
ΔAOI vuông tại O
=>AO^2+OI^2=AI^2
=>AI^2=4^2+3^2=25
=>AI=5cm
Xét ΔAOI vuông tại O và ΔAMB vuông tại M có
góc OAI chung
Do đó: ΔAOI đồng dạng với ΔAMB
=>AO/AM=AI/AB
=>4/AM=5/8
=>AM=4*8/5=6,4cm
ΔAMB vuông tại M
=>AM^2=AB^2+MB^2
=>MB^2=8^2-6,4^2=4,8^2
=>MB=4,8cm
ΔMAB vuông tại M có MH là đường cao
nên MH*AB=MB*MA
=>MH*8=4,8*6,4
=>MH=3,84(cm)
Cảm ơn ạ