Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

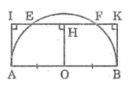
Ta có: AI ⊥ EF (gt)
BK ⊥ EF (gt)
Suy ra: AI // BK
Suy ra tứ giác ABKI là hình thang
Kẻ OH ⊥ EF
Suy ra: OH // AI // BK
Ta có: OA = OB (= R)
Suy ra: HI = HK
Hay: HE + EI = HF + FK (1)
Lại có: HE = HF (đường kính dây cung) (2)
Từ (1) và (2) suy ra: IE = KF

cho mình lm vs đề nửa đường tròn hén :
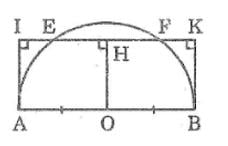
bn tk hình thay K là J thì nó cũng là hình đúm nuôn
Ta có : \(AI\perp EF\)(gt)
\(BJ\perp EF\left(gt\right)\)
=> AI//BJ
Suy ra tứ giác ABJI là hình thang
Kẻ OH ⊥ EF
Suy ra: OH // AI // BJ
Ta có: OA = OB (= R)
Suy ra: HI = HJ
Hay: HE + EI = HF + FJ (1)
Lại có: HE = HF (đường kính dây cung) (2)
Từ (1) và (2) suy ra: IE = JF

gọi O là tâm đường tròn đường kính AB
Kẻ OE vuông góc vs CD (E thuộc CD)
suy ra E là trung điểm của CD
Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song vs cạnh đáy)
suy ra EH=EK mà EC=ED Suy ra đpcm

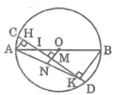
Kẻ OM ⊥ CD cắt AD tại N
Ta có: MC = MD (đường kính dây cung)
Hay MH + CH = MK + KD (1)
Ta có: OM // BK (cùng vuông góc với CD)
Hay: MN // BK
Mà: OA = OB (= R)
Suy ra: NA = NK (tính chất đường trung bình của tam giác)
Lại có: OM // AH (cùng vuông góc với CD)
Hay: MN // AH
Mà: NA = NK (chứng minh trên)
Suy ra: MH = MK (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: CH = DK

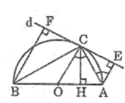
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên góc (ACB) = 90 °
Tam giác ABC vuông tại C có CH ⊥ AB
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
C H 2 = HA.HB (3)
Xét hai tam giác ACH và ACE, ta có:
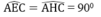
CH = CE (tính chất đường phân giác)
AC chung
Suy ra : ∆ ACH = ∆ ACE (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BCF, ta có:
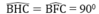
CH = CF (= CE)
BC chung
Suy ra: ∆ BCH = ∆ BCF (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: C H 2 = AE.BF

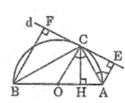
Ta có: OC ⊥ d (tính chất tiếp tuyến)
AE ⊥ d (gt)
BF ⊥ d (gt)
Suy ra : OC // AE // BF
Mà OA = OB (= R)
Suy ra: CE = CF (tính chất đường thẳng song song cách đều)

A O B H M K P C
Ta có : \(AH\perp CD\left(gt\right)\)
\(BK\perp CD\left(gt\right)\)
=> AH // BK
=> Tứ giác ABKH là hình thang có đáy AH và BK
Theo ( gt ) : OA = OB mà \(OM\perp CD\)( theo cách dựng )
=> OM // AC / BK
=> MK = MH (1)
Mặt khác : \(OM\perp CD\Rightarrow MC=MD\left(2\right)\)
Từ (1) và (2) => MH - MC = MK - MD
=> CH = DK
Vậy CH = DK

bạn ơi cho mình hỏi bước thứ nhất bạn làm theo định lí gì v bạn