Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có góc CBM là góc nội tiếp chắn cung CM
góc MBA là góc nội tiếp chắn cung MA
mà cung CM= cung MA( vì M là điểm chính giữa của cung CA)
=> góc CBM= góc MBA
hay BM là tia phân giác của góc CBA
CM tương tự ta có: AN là tia phân giác của góc CAB
xét tam giác CAB có
2 tia phân giác BM và AN cắt nhau tại I
=> I là tâm đường tròn nội tiếp tam giác CAB
=> CI là tia phân giác của góc ACB(đpcm)

a: sđ cung AC=2/3*180=120 độ
=>sđ cung AM=sđ cung MC=120/2=60 độ
sđ cung NB=sđ cung NC=60/2=30 độ
góc MIC=1/2(sđ cung AB+sđ cung MC)
=1/2(180+60)=120 độ
b: N là điểm chính giữa của cung BC
=>ON vuông góc bC
=>ON//AC
=>DN vuông góc NO
=>DN là tiếp tuyến của (O)

Bài 2: Cho nửa đường tròn (O) đường kính AB, điểm C thuộc nửa đường tròn có số đo bằng 60o. Gọi E, F lần lượt là điểm chính giữa của các cung AC và BC, I là giao điểm của AF và BE
a) Tính số đo các góc của .
b) Chứng minh: CI là phân giác của góc ACB
c) Chứng minh: Tứ giác ABFC là hình thang cân.
C thuộc nửa đường tròn có số đo bằng 60o tức là \(\widehat{AOC}\) hay \(\widehat{BOC}\) bằng 60o vậy bạn?


c) Vì F C H = F D H = 90 o nên tứ giác CHDF nội tiếp đường tròn tâm I đường kính FH
=> IC = ID. Mà OC = OD nên ∆ OCI = ∆ ODI (c.c.c) => COI = DOI
=> OI là phân giác của góc COD
d) Vì OC = CD = OD = R nên ∆ OCD đều => COD = 60o
Có C A D = 1 2 C O D = 30 o = > C F D = 90 o − C A D = 60 o
Xét góc nội tiếp và góc ở tâm cùng chắn cung CD của (I), có
CID = 2CFD = 120o => OIC = OID = C I D 2 = 60 o
Xét góc nội tiếp và góc ở tâm cùng chắn cung CD của (I), có
CID = 2CFD = 120o => OIC = OID = C I D 2 = 60 o
Mặt khác COI = DOI = C O D 2 = 30 o = > O I D + D O I = 90 o = > Δ O I D vuông tại D
Suy ra O I = O D sin 60 o = 2 R 3
Vậy I luôn thuộc đường tròn O ; 2 R 3

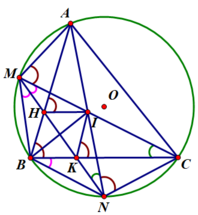
1) Chứng minh bốn điểm C, N, K, I cùng thuộc một đường tròn.
Ta có M là điểm chính giữa cung A B ⏜ ⇒ A M ⏜ = B M ⏜ ⇒ M N A ^ = M C B ^
⇒ K N I ^ = I C K ^ . Tứ giác CNKJ có C và N là 2 đỉnh kề nhau cùng nhìn cạnh KJ dưới góc bằng nhau nên CNKJ nội tiếp (dấu hiệu nhận biết tứ giác nội tiếp)
Do đó bốn điểm C, N, K, I cùng thuộc một đường tròn.