Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

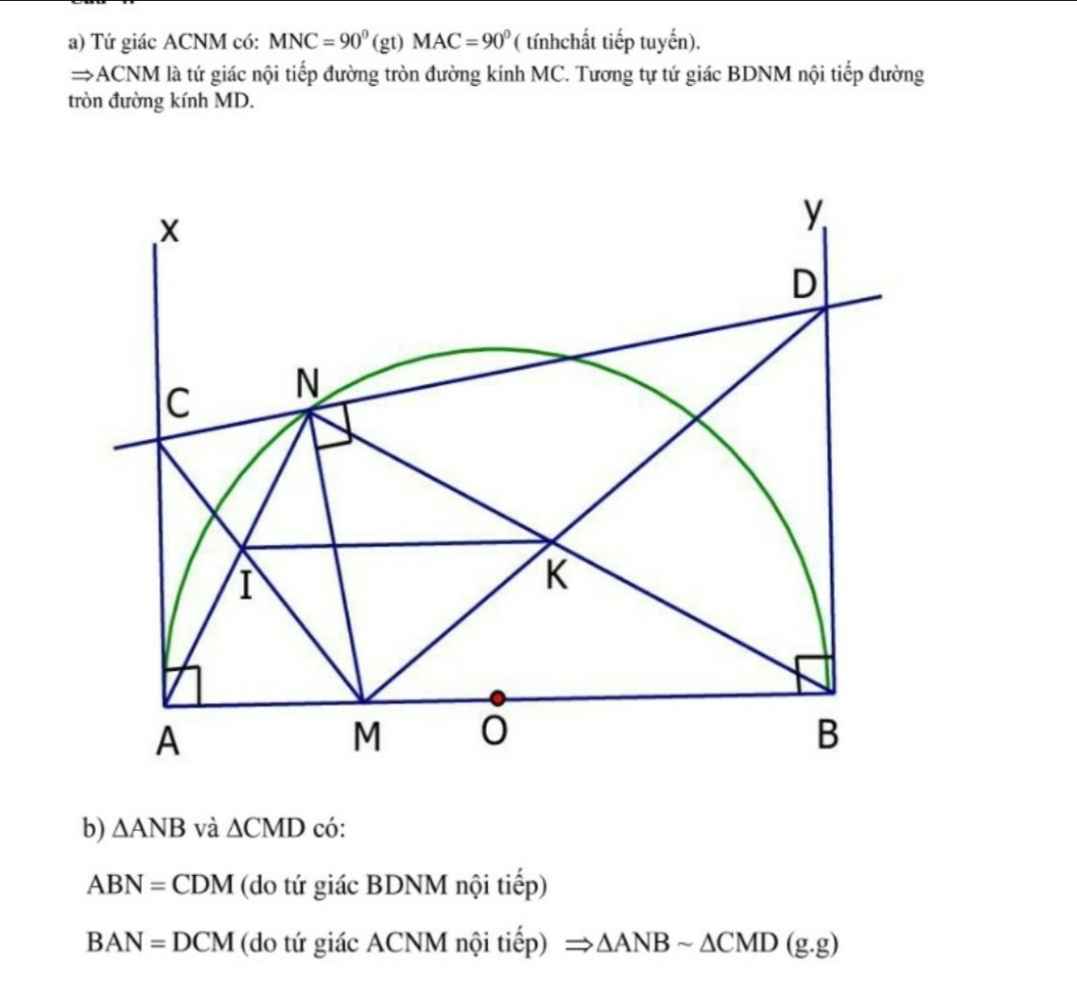
a, xét từ giác AMNC có
\(\widehat{CAM}\)=90∘CAM^=90∘ (Ac là tiếp tuyến của (O) , ˆ
\(\widehat{CNM}\)=90∘CNM^=90∘ (MN vuông góc với CD) => ˆ\(\widehat{CAM}+\widehat{CNM}\)=180
=> AMNC nội tiếp
Xét tứ giác BMND có ˆ\(\widehat{MNB}\)MBD^=90 ( BD là tiếp tuyến của (O) , \(\widehat{CND}\)=90 ( MN vuông góc với CD)
=> \(\widehat{MND}+\widehat{NAC}\)NAC^=180
=> Tứ giác BDMN nội tiếp
b, Ta có \(\widehat{CMN}=\widehat{NAC}\)NAC^ (cùng chắn CN)
=> \(\)\(\widehat{CMN}\)CMN^=1212 cung AN(1)
Ta cũng có\(\widehat{NMD}+\widehat{NMD}\)NBD^ (cùng chắn cung ND)
\(\widehat{NMD}\)=1212 cung NB(2)
Từ (1) và (2) => \(\widehat{CMD}+\widehat{NMD}\)NMD^= 1212 (cung AN + cung NB)
=> \(\widehat{CMD}\)= 1212 cung AB = 18021802=90
=> tam giác CMD vuông tại M
Vì NMBD nội tiếp => \(\widehat{NDM}+\widehat{NBM}\)NBM^ ( góc nội tiếp cùng chắn cung AM)
Mà \(\widehat{MCD}+\widehat{NBM}\)=90
=> \(\widehat{MCD}+\widehat{NBM}\)NBM^=90 (1)
Mặt khác \(\widehat{NAB}+\widehat{NBA}\)NBA^=90 (2)
Từ (1) và (2) => \(\widehat{MCD}=\widehat{NAB}\)
Xét tam giác ANB và CMD ta cs
\(\widehat{ANB}=\widehat{CMD}\) (=90)
\(\widehat{MCD}=\widehat{NAD}\)
=> 2 tam giác này bằng nhau

\(a,\\ \widehat{CAM}=\widehat{CNM}=90^0\\ \Rightarrow CNMA.là,tứ.giác.nội.tiếp\\ \widehat{MND}=\widehat{MBD}=90^0\\ \Rightarrow NMBF.là.tứ,giác.nội.tiếp\\ b,CNMA.nội.tiếp\\ \Rightarrow\widehat{NAM}=\widehat{NCM}\\ MNDB.nội.tiếp\\ \Rightarrow\widehat{NDM}=\widehat{NBM}\)
\(\Delta CMD.và.\Delta AnpNB:\\ \widehat{NAM}=\widehat{NCM};\widehat{NDM}=\widehat{ABM}\\ \Rightarrow\Delta....đồng.dạng.\Delta....\)