Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

VẼ HÌNH (chú thích : c là cùng / g là gốc /)
Ta có :cBC=cCD+cBD
:cAD=cCD+cAC
mà :cAD=cBC(gt)
Do do : cBD=cAD (1)
Ta có:gocCAB la goc noi tiep chan cBC (2)
:gocDBA la goc noi tiep chan cAD(3)
Từ(1),(2) va (3) suy ra :gocCAB=gocDBA
=> Tứ giác ACDB là hình thang cân(vì sd 2 gốc ở đay=nhau)

d) tam giác ABC dùng sin,cos,tan,cot gì đó tính ra CB và AC thì ta đước IB=CB
Xét tam giác KIB và tam giác ACB
có : AB=IB(tam giác IBC đều -cmt)
ACB=KIB=90
KBI=CBA(cùng chắn 2 cung bằng nhau)
=>hai tam giác bằng nhau
=> KI=AC
S=(KI+AB)*IB)/2
a) vì cung AC ,,cung CD , cung BD bằng nhau
=>góc COC=góc COD=góc BOD
mà tổng của chúng =180độ
=>mỗi góc = 60 độ
=>..............................

VE HINH
â) Xét tứ giác KCID ,co:
gocI = (cungAB+cungCD):2 = (180+60):2 = 120 độ
gocK=(cungAB-cungCD):2 =(180-60):2=60 độ
gócI+gocK=120do+60do=180 do
Vay : tứ giác KCID nội tiếp (tổng số đo 2 góc đối diện=180 độ )
:góc AKB = 60 độ
b)Ta có:AB//CD
=>cungAC=cungBD=(180-60):2=60 do (2 cung nằm giữa 2 dây song song thì = nhau )
=>AC=BD(2 dây chan 2 cung = nhau thi = nhau ) (1)
=>tứ giác ACDB là hình thang cân
***Xét : 3giac AKDva 3giac BKC ,co:
gocD=gocC=90do (vi gocC va gocD là góc nội tiếp chắn nửa đường tròn)
gocCAD=gocDBC(2goc noi tiep cung chan cungCD)
AD=BC(2 đường chéo của hình thang cân thì = nhau )(cmt)
Do do:3giacAKD =3giacBKC (g-c-g)
=>KD=KC (2 canh tương ứng) (2)
Ta lại có :KA=KC+AC(C nam giua A va K)
}(3)
:KB=KD+BD(D nam giua B va K)
Tu (1) ,(2) va (3) suy ra KA=KB (4)
Tu (2) va (4) suy ra KA.KC=KB.KD .

b)
+ Xét đt (o) có
tứ giác BFACN nội tiếp đt
\(\rightarrow ABC\)=AFC ( 2 góc nt cùng chắn cung AC)
CÓ :
BD là tiếp tuyến đt (o) tại B(gt)
\(\rightarrow\) BD vuông góc BO (TC tiếp tuyến)
\(\rightarrow\)BD vuông góc BC (O thuộc BC)
\(\rightarrow\) DBC = 90(dn)
\(\rightarrow\)tam giác DBC vuông tại B
xét tam giác vuông DBC cso
BDC+DCB=90(2 góc phụ nhau trong tg vuông) (1)
+Xét đt (o) có:
BAC= 90 ( góc nt chắn nửa dtđk BC)
\(\rightarrow\)tam giác BAC vuông tại A
Xét tam giác vuông BAC có
ABC+ACB=90 (2 gọc phụ nhau trong tam giác vuông)
\(\rightarrow\) ABC+DCB=90(A thuộc DC ) (2)
từ(1) và(2) \(\rightarrow\) BDC=ABC( cùng phụ DCB)
Mà AFC=ABC(CMT)
\(\rightarrow\) BDC=AFC(=ABC)
+Có :
AFC+AFE=180( 2 góc kề bù)
Mà 2 góc ở vị trí đối nhau
\(\rightarrow\) tứ giác DEFA nội tiếp ( DHNB tứ giác nội tiếp)
| |

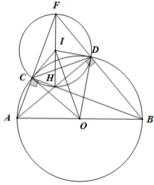
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B