Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S_1=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinB\)
\(S_2=\dfrac{1}{2}\cdot3\cdot BC\cdot\dfrac{1}{2}\cdot AB\cdot sinC=\dfrac{3}{4}\cdot BC\cdot AB\cdot sinC\)
=>\(\dfrac{S_2}{S_1}=\dfrac{3}{4}:\dfrac{1}{2}=\dfrac{3}{2}\)
=>Diện tích mới tạo thành bằng 3/2 lần diện tích cũ

Chiều cao là:
(25-7):2=9 (cm)
Cạnh đáy là:
9+7=16 (cm)
diện tích hình bình hành là:
16x9=144 (cm2)
đ/s :

Chọn D.
Diện tích tam giác ABC ban đầu là
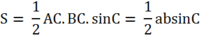
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là
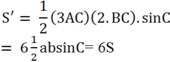

c: \(AM^2=\dfrac{2\cdot\left(AB^2+AC^2\right)-BC^2}{4}=\dfrac{2\cdot\left(48^2+14^2\right)-50^2}{4}=625\)
nên AM=25(cm)
a: Xét ΔAHB vuông tại H có
\(AB^2=AH^2+HB^2\)
nên AH=16(cm)
Xét ΔAHC vuông tại H và ΔBKC vuông tại K có
\(\widehat{C}\) chung
Do đó: ΔAHC\(\sim\)ΔBKC
Suy ra: \(\dfrac{AH}{BK}=\dfrac{HC}{KC}=\dfrac{AC}{BC}\)
=>16/BK=20/24=5/6
=>BK=19,2(cm)

a: BC: x+y+4=0
=>AH: -x+y+c=0
Thay x=-1 và y=-2 vào AH, ta được:
c+1-2=0
=>c=1
=>-x+y+1=0
=>x-y-1=0
b: BC: x+y+4=0
=>B(x;-x-4)
Tọa độ M là:
xM=(x-1)/2 và yM=(-x-4-2)/2=(-x-6)/2
BC: x+y+4=0
=>MN: x+y+c=0
Thay xM=(x-1)/2 và yM=(-x-6)/2 vào MN, ta được:
\(\dfrac{x-1}{2}+\dfrac{-x-6}{2}+c=0\)
=>c+(1/2x-1/2-1/2x-3)=0
=>c=7/2
=>x+y+7/2=0


