Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 thẻ trong số 6 thẻ.
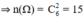
a. Gọi A: “ Hai điểm là đầu mút của cạnh của lục giác”
⇒ n(A) = 6 (Lục giác có 6 cạnh)
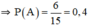
b. Gọi B: “ Hai điểm là đầu mút của đường chéo”
⇒ B = A− (Vì một đoạn thẳng chỉ có thể là một cạnh hoặc một đường chéo)
⇒ P(B) = 1 – P(A) = 1 – 0,4 = 0,6
c. Gọi C: “ Hai điểm là đầu mút của đường chéo nối hai đỉnh đối diện”
⇒ n(C) = 3
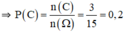

Chọn B
Gọi A là biến cố lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C)
Số đường chéo của đa giác đều 20 đỉnh là
C
20
2
- 20 = 170. Khi đó, ta có số cách lấy ra 2 đường chéo trong số 170 đường là ![]()
Để có hai đường chéo cắt nhau tại một điểm nằm trong đường tròn (C) thì hai đường chéo đó phải là đường chéo của tứ giác có 4 đỉnh là đỉnh của đa giác đều 20 đỉnh. Do đó, số cách lấy ra 2 đường chéo có giao điểm nằm trong đường tròn tâm O là C 20 4 = 4845
Vậy xác suất lấy ra hai đường chéo có giao điểm nằm trong đường tròn (C) là
![]()

Ta cần chứng minh tam giác MNP là tam giác cân và có một góc bằng \(\frac{\Pi}{3}\)
Giả sử lục giacs có hướng âm, kí hiệu \(f\) là phép quay vec tơ theo góc \(-\frac{\Pi}{3}\) và M, N. P theo thứ tự là trung điểm FA, BC, DE
Khi đó AB=BO, CD=DO=OC, EF=FO=OE nên các tam giác ABO, CDO, EFO đều và có hướng âm
Suy ra \(f\left(\overrightarrow{AB}\right)=\overrightarrow{AO}\), \(f\left(\overrightarrow{OC}\right)=\overrightarrow{OD}\), \(f\left(\overrightarrow{FO}\right)=\overrightarrow{FE}\)
Từ đó ta có :
\(f\left(\overrightarrow{MN}\right)=f\left(\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{FC}\right)\right)=\frac{1}{2}\left(f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{FC}\right)\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AO}\right)+\overrightarrow{OD}+\overrightarrow{FE}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{FE}\right)\)
\(=\overrightarrow{MP}\)
Suy ra tam giác MNP cân và có góc PMN = \(\frac{\Pi}{3}\) => Điều phải chứng minh

a.Không gian mẫu gồm 12 phần tử, được mô tả:
Ω = {(1, 2), (2; 1); (1, 3), (3; 1); (1, 4), (4; 1); (2, 3), (3; 2); (2, 4), (4; 2); (3, 4); ( 4, 3)}
Trong đó (i, j) là kết quả "lần đầu lấy trúng thẻ i và lần 2 lấy trúng thẻ j".
b.Xác định các biến cố sau:
A: "Tổng các số trên hai thẻ là số chẵn".
⇒ A = {(1, 3), (3; 1); (2, 4); (4; 2)}
B: "Tích các số trên hai thẻ là số chẵn."
⇒ B = {(1, 2), (2; 1); (1, 4), (4; 1); (2, 3), (3; 2); (2, 4),(4; 2); (3, 4); (4; 3)}

Phép thử T được xét là: "Từ hộp đã cho, lấy ngẫu nhiên hai thẻ".
a) Đồng nhất mỗi thẻ với chữ số ghi trên thẻ đó, ta có: Mỗi một kết quả có thể có các phép thử là một tổ hợp chập 2 của 4 chữ số 1, 2, 3, 4. Do đó, số phần tử của không gian mẫu là C24 = 6, và không gian mẫu gồm các phần tử sau:
Ω = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}.
b) A = {(1, 3), (2, 4)}.
B = {(1, 2), (1, 4), (2, 3), (2, 4), (3, 4)} = Ω {(1, 3)}

Lấy ngẫu nhiên đồng thời 2 thẻ trong tổng số 50 thẻ từ hộp có \({C}_{50}^2 = 1225\) cách.
a) Gọi \(C\) là biến cố “2 thẻ lấy ra là số chẵn”, \(D\) là biến cố “2 thẻ lấy ra là số lẻ”
\( \Rightarrow A = C \cup D\)
Lấy ngẫu nhiên đồng thời 2 thẻ trong tổng số 25 thẻ chẵn có \({C}_{25}^2 = 300\) cách
\( \Rightarrow n\left( C \right) = 300 \Rightarrow P\left( C \right) = \frac{{n\left( C \right)}}{{n\left( \Omega \right)}} = \frac{{300}}{{1225}} = \frac{{12}}{{49}}\)
Lấy ngẫu nhiên đồng thời 2 thẻ trong tổng số 25 thẻ lẻ có \({C}_{25}^2 = 300\) cách
\( \Rightarrow n\left( D \right) = 300 \Rightarrow P\left( C \right) = \frac{{n\left( D \right)}}{{n\left( \Omega \right)}} = \frac{{300}}{{1225}} = \frac{{12}}{{49}}\)
Vì \(C\) và \(D\) là hai biến cố xung khắc nên \(P\left( A \right) = P\left( C \right) + P\left( D \right) = \frac{{12}}{{49}} + \frac{{12}}{{49}} = \frac{{24}}{{49}}\)
b) Gọi \(E\) là biến cố “1 thẻ chia hết cho 4, 1 thẻ là số lẻ”
\( \Rightarrow B = C \cup E\)
Lấy ngẫu nhiên 1 thẻ trong tổng số 12 thẻ chia hết cho 4 có \({C}_{12}^1 = 12\) cách
Lấy ngẫu nhiên 1 thẻ trong tổng số 25 thẻ lẻ có \({C}_{25}^1 = 25\) cách
\( \Rightarrow n\left( E \right) = 12.25 = 300 \Rightarrow P\left( E \right) = \frac{{n\left( E \right)}}{{n\left(\Omega \right)}} = \frac{{300}}{{1225}} = \frac{{12}}{{49}}\)
Vì \(C\) và \(E\) là hai biến cố xung khắc nên \(P\left( B \right) = P\left( C \right) + P\left( E \right) = \frac{{12}}{{49}} + \frac{{12}}{{49}} = \frac{{24}}{{49}}\)

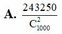


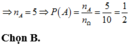
Giải:
Vì lấy 2 điểm nên:
\(C^2_6=15\rightarrow n\left(\Omega\right)=15\)
Gọi:
\(A\) là biến cố "2 thẻ lấy ra là 2 cạnh của lục giác"
\(B\) là biến cố "2 thẻ lấy ra là đường chéo của lục giác"
\(C\) là biến cố "2 thẻ lấy ra là đường chéo của 2 cạnh đối diện của lục giác"
a) \(n\left(A\right)=6\Rightarrow P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{6}{15}=\dfrac{2}{5}\)
b) \(B=\overline{A}\Rightarrow P\left(B\right)=1-P\left(A\right)=1-\dfrac{2}{5}=\dfrac{3}{5}\)
c) \(n\left(C\right)=6\Rightarrow P\left(C\right)=\dfrac{n\left(C\right)}{n\left(\Omega\right)}=\dfrac{3}{15}=\dfrac{1}{5}\)