Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Nguyễn Thị Kim Diệp dụ mình k
a b c A B 1 2 1 2 c z I X
+ a // b
∠ aAb slt ∠ cBA
=> ∠ aAb = ∠ cBA (tc) (1)
+ AI là pg của ∠ aAB => ∠ A1 = ∠ aAB : 2 (2)
+ BX là pg của ∠ cBA => ∠ B1 = ∠ cBA : 2 (3)
(1)(2)(3) => ∠ A1 = ∠ B1 mà ∠ A1 slt ∠ B1
nên BX // AI
- Gỉa sử 2 góc đồng vị đó là a và b có tia phân giác cắt tạo thành các góc a1, a2, b1, b2
Thấy : \(\widehat{a}=\widehat{b}\)
Mà \(\left\{{}\begin{matrix}\widehat{a1}=\widehat{a2}\\\widehat{b1}=\widehat{b2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{a1}=\widehat{b1}\\\widehat{a2}=\widehat{b2}\end{matrix}\right.\)
- Xét 2 đường phân giác có 2 góc a1, b1 hoặc a2, b2 là 2 góc ở vị trí đồng vị và bằng nhau .
=> Hai đường phân giác đó song song với nhau .
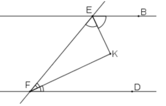
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F
Ta có: ∠BEF + ∠EFD = 180o (hai góc trong cùng phía)
+) Do EK là tia phân giác của góc ∠ BEF nên:
∠E1 = 1/2 .∠ (BEF) (1)
+) Do FK là tia phân giác của góc EFD nên :
∠F1 = 1/2 .∠EFD (2)
Từ (1) và (2) suy ra:
∠E1 +∠F1 =1/2 .(∠BEF + ∠EFD ) = 1/2 . 180º = 90º ( ∠BEF + ∠EFD = 180º hai góc trong cùng phía)
Trong ΔEKF,ta có:
∠EKF = 180o-(∠E1 + ∠F1) = 180o-90o=90o
Vậy EK ⊥FK
