VB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 6 2023
a: NP^2=MN^2+MP^2
=>ΔMNP vuông tại M
b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
góc MND=góc END
=>ΔNMD=ΔNED
=>DM=DE
KV
9 tháng 5 2023
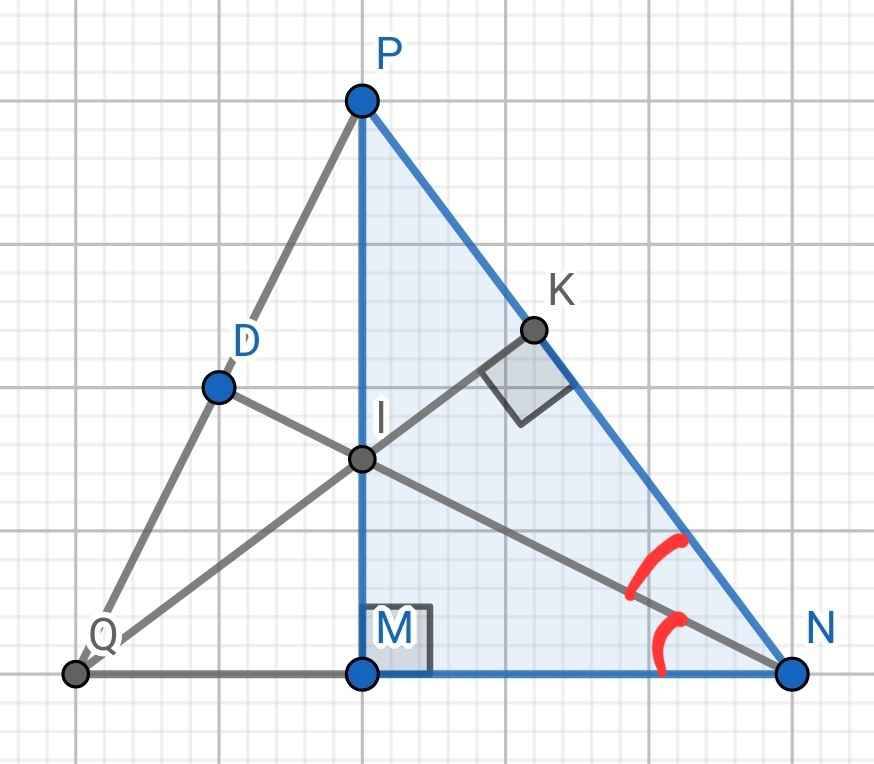
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
9 tháng 12 2016
Ta có hình vẽ
M N P I
a/ Xét tam giác MNI và tam giác MPI có:
MN = MP (GT)
\(\widehat{NMI}\)=\(\widehat{PMI}\) (GT)
MI: cạnh chung
=> tam giác MNI = tam giác MPI (c.g.c)
=> NI = IP (2 cạnh tương ứng)
b/ Ta có: tam giác MNI = tam giác MPI (câu a)
=> \(\widehat{MIN}\)=\(\widehat{MIP}\) (2 góc tương ứng)
Mà \(\widehat{MIN}\)+\(\widehat{MIP}\)=1800 (kề bù)
=> \(\widehat{MIN}\)=\(\widehat{MIP}\)=900
=> MI \(\perp\)NP (đpcm)
19 tháng 1 2019
a) Xét \(\Delta\)ANM và \(\Delta\)ABM có :
- MN = MB ( gt )
- Góc AMN = góc AMB ( vì MA là phân giác )
- MA : cạnh chung
\(\Rightarrow\)\(\Delta\)ANM = \(\Delta\)ABM ( c . g . c )
\(\Rightarrow\)AN = AB ( hai cạnh tương ứng )
b) Gọi giao điểm giữa NB và MA là I
Xét \(\Delta\)INM và \(\Delta\)IBM có :
- MN = MB ( gt )
- Góc IMN = góc IMB ( vì MI là phân giác )
- MI : cạnh chung
\(\Rightarrow\)\(\Delta\)INM = \(\Delta\)IBM ( c . g . c )
\(\Rightarrow\)Góc MIN = góc MIB ( hai góc tương ứng )
Mà góc MIN + góc MIB = 180 ( do kề bù )
nên góc MIN = góc MIB = 180 ÷ 2 = 90 độ hay NB vuông góc với MA .
LB
11 tháng 5 2017
a)
Xét tam giác END và tam giác MND, có
\(\widehat{MND}=\widehat{DNE}=30^o\)(vì ND là tia phân giác)
\(\widehat{M}=\widehat{E}=90^o\)
ND là cạnh chung
\(\Rightarrow\Delta END=\Delta MND\)
\(\RightarrowĐPCM\)
6 tháng 3 2022
a: Xét ΔMNQ vuông tại M và ΔHNQ vuông tại H có
NQ chung
\(\widehat{MNQ}=\widehat{HNQ}\)
Do đó: ΔMNQ=ΔHNQ
b: ta có: ΔMNQ=ΔHNQ
nên NM=NH
hay ΔNHM cân tại N
mà \(\widehat{MNH}=60^0\)
nên ΔNHM đều