Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đây là cách trình bày
(a + b) +c = (a + c) +b
Bạn có thể thay đổi vị trí của bất cứ số nào trong phép tính cộng mà không có ảnh hưởng đến kết quả
VD (1 + 2) + 3 = (1 +3) + 2 = 6
ht

Gọi số tuổi của bố là x thì :
=> tuổi mẹ = x - 1
=> tuổi con = 60 - (x + x - 1)
ta có phương trình: (x + x -1) - (60 - x - x +1) =58
<=> x = 30
Vậy tuổi bố = 30
Tuổi mẹ = 30 -1 = 29
Tuổi con = 60 - (30 + 30 -1) = 1

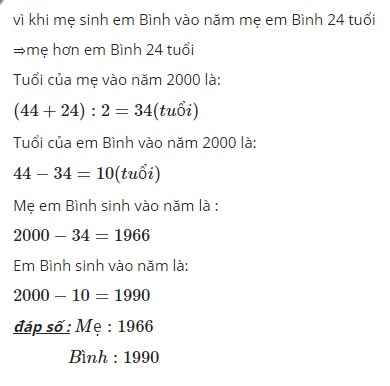
tuổi bình năm 2000
( 44- 24) : 2 = 10 (tuổi)
tuoiỉ mẹ năm 2000 là
44 - 10 = 34 (tuổi)
Bình sinh năm là
2000 - 10 = 1990 (năm)

tổng=1200l
bồn nhỏ có số l nc là:1200:(5+7)x5=500l
bồn to có số l nước là 1200-500=700l
ta có sơ đồ
bồn bé ------ 1200 lít
bồn bồn lớn ------
bồn bé có số lít là:
1200:(5+7)x5=500(lít)
bồn lớn có số lít là:
1200-500=700 (lít)
đáp số :bồn bé:500 lít nước
bồn lớn :700 lit nước

Gọi số cần tìm là abcd (abcd E N,a khác 0)
Vì số cần tìm là số tự nhiên
mà số đó cộng số các c/s và cộng tổng các c/s của nó
=>số cần tìm phải có 4 c/s
=>Theo đề bài ta có
abcd+4+a+b+c+d=1988
abcd+a+b+c+d=1984
Vậy a=1,b=9,c=0,d=2

a: =3/2-7/8=12/8-7/8=5/8
b: =15/7-48/42+5/6=90/42-48/42+35/42=77/42=11/6
c: =5/3-3/4-2/5=100/60-45/60-24/60=31/60
sao cậu ko tick cho bạn ấy
ko phải cậu bảo sẽ tick sao
cậu nói dối nhiều vậy không sợ bị người khác nói xấu mình sao

1. Ví dụ về tính chất kết hợp của phép cộng. Khi cộng một tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
1. Tính chất phép cộng các số nguyên
a. Tính chất giao hoán: a+b=b+a.a+b=b+a.
b. Tính chất kết hợp: (a+b)+c=a+(b+c).(a+b)+c=a+(b+c).
Lưu ý: (a+b)+c(a+b)+c được gọi là tổng của ba số a,b,ca,b,c và được viết đơn giản là a+b+c.a+b+c.
c. Cộng với số 0: a+0=a.a+0=a.
d. Cộng với số đối: a+(−a)=0.a+(−a)=0.
Ví dụ:
+) Giao hoán: 4+(−3)=(−3)+44+(−3)=(−3)+4
+) Kết hợp: (10+22)+(−10)=[10+(−10)]+22(10+22)+(−10)=[10+(−10)]+22
+) Cộng với số 0: 5+0=0+5=55+0=0+5=5
+) Cộng với số đối: 31+(−31)=031+(−31)=0
+) Tính chất phân phối: 4(12+24)=4.12+4.244(12+24)=4.12+4.24
2. Các dạng toán cơ bản
Dạng 1: Tính tổng các nhiều số nguyên cho trước
Phương pháp:
Tùy từng bài, ta có thể giải theo các cách sau :
- Áp dụng tính chất giao hoán và kết hợp của phép cộng
- Cộng dần hai số một
- Cộng các số dương với nhau, cộng các số âm với nhau, cuối cùng cộng hai kết quả trên
Dạng 2 : Tính tổng tất cả các số nguyên thuộc một khoảng cho trước
Phương pháp:
- Liệt kê tất cả các số nguyên trong khoảng cho trước
- Tính tổng tất cả các số nguyên đó, chú ý nhóm từng cặp số đối nhau. oki bạn nhé cho mình 1