Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi P là trung điểm MN \(\Rightarrow P\left(0;-1\right)\)
\(\overrightarrow{MN}=\left(2;-4\right)=2\left(1;-2\right)\Rightarrow\) trung trực của MN nhận (1;-2) là 1 vtpt
Phương trình trung trực MN:
\(1\left(x-0\right)-2\left(y+1\right)=0\Leftrightarrow x-2y-2=0\)
Gọi I là tâm đường tròn cần tìm \(\Rightarrow\) I là giao điểm của d và trung trực MN
Tọa độ I thỏa mãn: \(\left\{{}\begin{matrix}x-2y-2=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow I\left(-\dfrac{4}{3};-\dfrac{5}{3}\right)\)
\(\overrightarrow{IM}=\left(\dfrac{1}{3};\dfrac{8}{3}\right)\Rightarrow R^2=IM^2=\dfrac{65}{9}\)
Phương trình: \(\left(x+\dfrac{4}{3}\right)^2+\left(y+\dfrac{5}{3}\right)^2=\dfrac{65}{9}\)

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
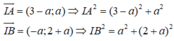
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
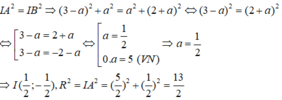
Vậy phương trình đường tròn có dạng:
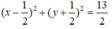
Ta có:
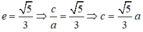
Giả sử elip (E) có dạng:
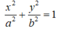
Vì (E) đi qua B nên:
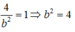
Mà
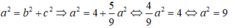
Vậy phương trình chính tắc của elip (E) là:
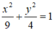

1.
\(\left(C\right):x^2+y^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=5\)
Đường tròn \(\left(C\right)\) có tâm \(I=\left(1;0\right)\), bán kính \(R=\sqrt{5}\)
Phương trình đường thẳng \(d_1\) có dạng: \(x+y+m=0\left(m\in R\right)\)
Mà \(d_1\) tiếp xúc với \(\left(C\right)\Rightarrow d\left(I;d_1\right)=\dfrac{\left|1+m\right|}{\sqrt{2}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+1\right|=\sqrt{10}\)
\(\Leftrightarrow m=-1\pm\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}d_1:x+y-1+\sqrt{10}=0\\d_1:x+y-1-\sqrt{10}=0\end{matrix}\right.\)
2.
Phương trình đường thẳng \(\Delta\) có dạng: \(x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;\Delta\right)=\sqrt{R^2-\dfrac{MN^2}{4}}=2\)
\(\Leftrightarrow\dfrac{\left|m+1\right|}{\sqrt{2}}=2\)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:x-y+1+2\sqrt{2}=0\\\Delta:x-y+1-2\sqrt{2}=0\end{matrix}\right.\)

I nằm trên d nên I(x;-2x-5)
IA=IB=R
=>(x-1)^2+(-2x-5+3)^2=(x+3)^2+(-2x-5-1)^2
=>x^2-2x+1+4x^2+8x+4=x^2+6x+9+4x^2+24x+36
=>6x+5=30x+45
=>-24x=40
=>x=-5/3
=>I(-5/3;-5/3)
A(1;-3)
=>R=4/3*căn 5
=>(C): (x+5/3)^2+(y+5/3)^2=80/9

Ta có : Đường thẳng I cách đều 2 đường thẳng d và denta
\(\Rightarrow\dfrac{\left|2x+y-3\right|}{\sqrt{5}}=\dfrac{\left|4x+2y-1\right|}{2\sqrt{5}}\)
\(\Rightarrow2\left|2x+y-3\right|=\left|4x+2y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+2y-6=4x+2y-1\\4x+2y-6=-4x-2y+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-6=1\left(L\right)\\8x+4y-7=0\end{matrix}\right.\)
\(\Leftrightarrow-\dfrac{8}{7}+\left(-\dfrac{4}{7}\right)+1=0\)
\(\Rightarrow a+b=-\dfrac{8}{7}-\dfrac{4}{7}=-\dfrac{12}{7}\)
Vậy ..
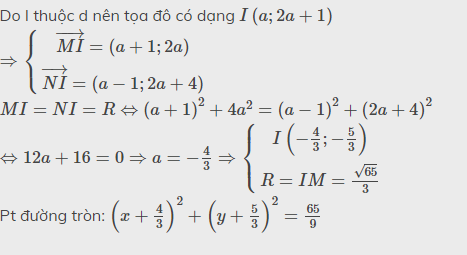

I nằm trên Δ nên I(x;2x+1)
\(IA=IB\)
=>IA^2=IB^2
=>(x+1)^2+(2x+1-1)^2=(x-1)^2+(2x+1+3)^2
=>x^2+2x+1+4x^2=x^2-2x+1+4x^2+16x+16
=>14x+17=2x+1
=>12x=-16
=>x=-4/3
=>I(-4/3;-5/3)
mà A(-1;1)
nên \(R=\sqrt{\left(-1+\dfrac{4}{3}\right)^2+\left(1+\dfrac{5}{3}\right)^2}=\dfrac{\sqrt{65}}{3}\)
=>\(\left(C\right):\left(x+\dfrac{4}{3}\right)^2+\left(y+\dfrac{5}{3}\right)^2=\dfrac{65}{9}\)