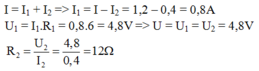Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định luật Ôm : \(I=\dfrac{U}{R}\)
=> \(U_1=R_1.I_1=7,2V\)
Không có hình cụ thể thì cho giả định : \(U_1=U_{tm}=7,2V\)
Điện trở R2 là :
\(I_2=\dfrac{U_{tm}}{R_2}=>R_2=\dfrac{U_{tm}}{I_2}=18\Omega\)
Tóm tắt:
R1 = 6ohm
I = 1,2A
I2 = 0,4A
------------------
R2 =?ohm
Giai:
Vì I khác I2 (1,2 khác 0,4) nên đây là đoạn mạch song song.
Cường độ dòng điện đi qua điện trở R1 là:
I = I1 + I2 => I1 = I - I2 = 1,2 - 0,4 = 0,8 (A)
Vì là mạch song song nên ta có:
U1 = U2 hay I1.R1 = I2.R2 => R2 = (I1.R1)/I2 = (0,8.6)/0,4 = 12 (om)
Vậy điện trở R2 là 12ohm.

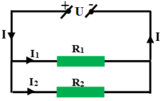
R 1 và R 2 mắc song song nên:
I = I 1 + I 2 → I 1 = I - I 2 = 1,2 – 0,4 = 0,8A
Và 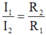
Và U = U 2 = U 1 = I 1 . R 1 = 0,8.6 = 4,8V
→ Điện trở
R
2
là: 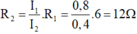

Hiệu điện thế U đặt vào hai đầu đoạn mạch là:
U = U 1 = U 2 = I 2 . R 2 = 0,4.12 = 4,8V

Vì R 3 song song với R 1 và R 2 nên:
U = U 1 = U 2 = U 3 = 4,8V
I = I 1 + I 2 + I 3 → I 3 = I - I 1 - I 2 = 1,5 – 0,8 – 0,4 = 0,3A
Điện trở
R
3
bằng: 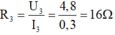
Điện trở tương đương của toàn mạch là: 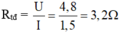

a) Rtd= \(\frac{1}{R_1}+\frac{1}{R_2}\)= \(\frac{1}{15}+\frac{1}{10}\)=6 \(\Omega\)
b) I=\(\frac{U}{R}\)(định luật ôm)=\(\frac{18}{6}\)=3(A)

a) Chập M và N lại ta có mạch ((R3//R4)ntR2)//R1
R342=\(\dfrac{R3.R4}{R3+R4+RR2=}+R2=\dfrac{6.6}{6+6}+9=12\Omega\)
Rtđ=\(\dfrac{R342.R1}{R342+R1}=6\Omega\)
=>\(I=\dfrac{U}{Rt\text{đ}}=\dfrac{24}{6}=4A\)
Vì R342//R1=>U342=U1=U=24V
=> \(I1=\dfrac{U1}{R1}=\dfrac{24}{12}=2A\)
Vì R23ntR2=>I34=I2=I342=\(\dfrac{U342}{R342}=\dfrac{24}{12}=2A\)
Vì R3//R4=>U3=U4=U34=I34.R34=2.3=6V
=>I3=\(\dfrac{U3}{R3}=\dfrac{6}{6}=1A\)
Ta lại có Ia=I1+I3=3A

ta có:
I=I1=I2=I3=2A
U=U1 + U2 + U3
\(\Leftrightarrow90=2R_1+2R_2+2R_3\)
Mà R1=R2=4R3
\(\Rightarrow2R_1+2R_1+8R_1=90\)
giải phương trình ta có:R1=7.5\(\Omega\)
\(\Rightarrow R_2=7.5\Omega\)
\(\Rightarrow R_3=30\Omega\)