Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\left|\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\right|=2\cdot AC=2\cdot5=10\)
b: \(\left|\overrightarrow{AM}+\overrightarrow{AN}\right|=\left|\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{2}+\dfrac{\overrightarrow{AD}+\overrightarrow{AC}}{2}\right|\)
\(=\left|\dfrac{3\cdot\overrightarrow{AC}}{2}\right|=\dfrac{3}{2}AC=\dfrac{3}{2}\cdot5=\dfrac{15}{2}=7.5\)

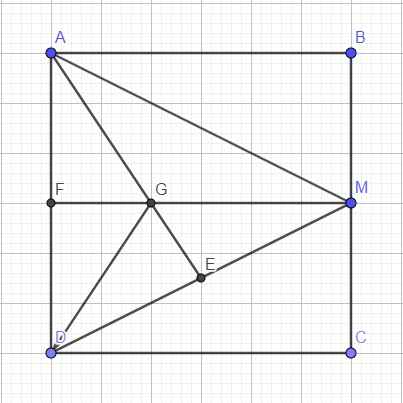
\(\left\{{}\begin{matrix}AM=\sqrt{AB^2+BM^2}=3\sqrt{5}\\DM=\sqrt{CD^2+CM^2}=3\sqrt{5}\end{matrix}\right.\) \(\Rightarrow\) tam giác ADM cân tại M
Gọi F là trung điểm AD \(\Rightarrow ABMF\) là hình chữ nhật \(\Rightarrow MF=AB=6\)
Theo tính chất trọng tâm: \(GF=\dfrac{1}{3}MF=2\)
\(DF=\dfrac{1}{2}AD=3\)
Đặt \(T=\left|\overrightarrow{GD}\right|=\left|\overrightarrow{GF}+\overrightarrow{FD}\right|\)
\(\Rightarrow T^2=GF^2+FD^2+2\overrightarrow{GF}.\overrightarrow{DF}=GF^2+DF^2=2^2+3^2=13\)
\(\Rightarrow\left|\overrightarrow{GD}\right|=\sqrt{13}\)

Lấy điểm F sao cho DF // AM và F thuộc BC
Theo quy tắc hình bình hành ( AM//DF ; AD //MF)
\(\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{AM}\)
Vì AMFD là hình bình hành nên \(\left|\overrightarrow{AD}\right|=\left|\overrightarrow{MF}\right|\Rightarrow BF=\frac{a}{2}+a=\frac{3a}{2}\)
Theo định lý Pytago ta có:
\(\left|\overrightarrow{AF}\right|^2=a^2+\left(\frac{3a}{2}\right)^2=a^2+\frac{9a^2}{4}=\frac{13a^2}{4}\)
\(\Rightarrow\left|\overrightarrow{AF}\right|=\sqrt{\frac{13a^2}{4}}=\frac{a\sqrt{13}}{2}\)
Dễ tính được \(AM=\frac{\sqrt{5}a}{2}\)
Ta thấy M là trung điểm của BC tức \(MB=MC=\frac{1}{2}BC=\frac{1}{2}AB\Rightarrow\widehat{AMB}=60^0\)
\(AD//BC\Rightarrow\widehat{DAC}=\widehat{AMB}=60^0\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{AM}=\sqrt{a^2+\frac{5a^2}{4}-2\cdot a\cdot\frac{\sqrt{5}a}{2}\cdot\cos120}\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{AM}=\sqrt{\frac{9a^2}{4}+\frac{\sqrt{5}a^2}{2}}=\sqrt{\frac{9a^2+2\sqrt{5}a^2}{4}}=\frac{a}{2}\sqrt{9+2\sqrt{5}}\)
Chắc vậy ạ
Sai thì thông cảm mk nha

HD: \(\overrightarrow{BC}=\frac{-2}{3}\overrightarrow{AM}+\frac{4}{3}\overrightarrow{AN};\overrightarrow{CD}=\frac{-4}{3}\overrightarrow{AM}+\frac{2}{3}\overrightarrow{AN}\)

hình :
A B C D E M 3 3 3 3
* ta kẻ hình bình hành \(ABEM\)
\(\Rightarrow\) \(\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{AE}\) (qui tắc hình bình hành)
\(\Rightarrow\left|\overrightarrow{AM}+\overrightarrow{AB}\right|=\overrightarrow{AE}=AE\)
ta có : \(ME=AB=3\) (2 cảnh đối của hình bình hành \(ABEM\))
và \(DM=\dfrac{1}{2}DC=\dfrac{1}{2}.3=\dfrac{3}{2}\)
\(\Rightarrow DE=DM+ME=\dfrac{3}{2}+3=\dfrac{9}{2}\)
xét tam giác vuông \(ADE\)
ta có : \(AE^2=DA^2+DE^2\Leftrightarrow AE=\sqrt{DA^2+DE^2}\)
\(AE=\sqrt{3^2+\left(\dfrac{9}{2}\right)^2}=\dfrac{3\sqrt{13}}{2}\)
vậy \(\left|\overrightarrow{AM}+\overrightarrow{AB}\right|=\overrightarrow{AE}=AE=\dfrac{3\sqrt{13}}{2}\)

a) N trung điểm AD \(\Rightarrow AN=\frac{AD}{2}=\frac{BC}{2}\)
M trung điểm BC \(\Rightarrow MC=\frac{BC}{2}\Rightarrow AN=MC\)mà AN//MC
nên AMCN là hình bình hành \(\Rightarrow\overrightarrow{AM}=\overrightarrow{NC}\)
b) Tương tự câu a ta được \(\hept{\begin{cases}ND=BM=\frac{1}{2}BC\\ND//BM\end{cases}}\)=> NDMB là hình bình hành=> NB//DM (1)
Xét 2 tam giác ANI và NDK: \(\hept{\begin{cases}AN=ND=\frac{AD}{2}\\\widehat{NAI}=\widehat{DNK}\left(AM//NC\right)\\\widehat{ANI}=\widehat{NDK}\left(NB//MD\right)\end{cases}\Rightarrow\Delta ANI=\Delta NDK\left(g.c.g\right)}\)
\(\Rightarrow NI=DK\)(2)
(1), (2) => \(\overrightarrow{NI}=\overrightarrow{DK}\)
\(\overrightarrow{AM}\cdot\overrightarrow{BC}=\overrightarrow{BC}\left(\overrightarrow{BM}-\overrightarrow{BA}\right)=\overrightarrow{BM}\cdot\overrightarrow{BC}-\overrightarrow{BC}\cdot\overrightarrow{BA}\)
\(=BM\cdot BC\cdot cos0^0=\dfrac{1}{2}\cdot a^2\cdot1=\dfrac{1}{2}a^2\)
\(\left|\overrightarrow{AM}+\overrightarrow{BC}\right|=\sqrt{AM^2+BC^2+2\cdot\dfrac{1}{2}a^2}\)
\(=\sqrt{\dfrac{1}{4}a^2+a^2+a^2+a^2}=\dfrac{\sqrt{13}}{2}\cdot a\)