Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

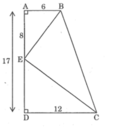
Ta có: AD = AE + DE
Suy ra: DE = AD – AE = 17 – 8 = 9cm
Xét △ ABE và △ DEC, ta có:
∠ A = ∠ D = 90 0 (1)
Mà :
Suy ra: 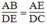 (2)
(2)
Từ (1) và (2) suy ra : △ ABE đồng dạng △ DEC (c.g.c)
Suy ra: ∠ ABE = ∠ DEC
Trong △ ABE ta có: ∠ A = 90 0 ⇒ ∠ (AEB) + ∠ (ABE) = 90 0
Suy ra: ∠ (AEB) + ∠ (DEC) = 90 0
Lại có: ∠ (AEB) + ∠ (BEC) + ∠ (DEC) = 180 0 (kề bù)
Vậy : ∠ (BEC) = 180 0 - ( ∠ (AEB) + ∠ (DEC)) = 180 0 - 90 0 = 90 0

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
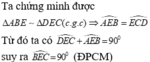
BEC=90