Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi

A B C D M N P Q
Tam giác BCD có :
BN = NC ( gt )
DP = PC ( gt )
\(\Rightarrow\)NP là đường trung bình tam giác BCD ( 1 )
Tam giác ADB có :
AQ = QD ( gt )
AM = MB ( gt )
\(\Rightarrow\)QM là đường trung bình tam giác ADB ( 2 )
Từ ( 1 ) , ( 2 ) suy ra NP = QM , NP // QM
\(\Rightarrow\)MNEF là hình bình hành ( đến đây bạn tự chứng minh tiếp hình thoi )
c) Để MNPQ là hình vuông thì ta chứng minh ABCD là hình thang cân có 2 đường chéo vuông góc với nhau

tgiác ABC có MN là đường trung bình => MN // AC và MN = AC/2
tgiác DAC có PQ là đường trung bình => PQ // AC và PQ = AC/2
vậy: MN // PQ và MN = PQ => MNPQ là hình bình hành
mặt khác xét tương tự cho hai tgiác ABD và CBD ta cũng có:
NP // BD và NP = BD/2
do giả thiết AC_|_BD => AC_|_NP mà MN // AC => MN_|_NP
tóm lại MNPQ là hình chữ nhật (hbh có một góc vuông)
b) MNPQ là hình vuông <=> MN = NP <=> AC/2 = BD/2 <=> AC = BD
vậy điều kiện là: tứ giác ABCD có hai đường chéo vuông góc và bằng nhau
c, Vỳ Mn là đườq trung bình của tam giác ABC nên MN= \(\frac{1}{2}\) AC= 3cm
QM là đường trung bình của tam giác ABD nên QM = \(\frac{1}{2}\) BD = 4cm
Mà MNPQ là hình chữ nhật nên diện tích ABCD = ( MN+PQ).2= (3.4):2 = 6cm
Bạn ơi lẽ ra chỗ diện tích hcn là phải bằng = 3 . 4 = 12cm chứ nhỉ bạn

a,
Xét ABD, ta có :
MA = MB (gt)
QA = QD (gt)
=> MQ là đường trung bình.
=> MQ // BD và MQ = BD : 2 (1)
Cmtt, ta được :
NP // BD và NP = BD : 2 (2)
NM // AC và NM = AC : 2 (3)
Từ (1) và (2) : MQ // NP và MQ = PP
=> Tứ giác MNPQ làhình bình hành.
ta có :
AC = BD ( hai đường chéo hình thang cân ABCD)
NM = AC : 2 (cmt)
MQ = BD : 2 (cmt)
=> NM = MQ
Xét hình bình hành MNPQ, ta có :
NM = MQ (cmt)
=> hình bình hành MNPQ là hình thoi.
b , Nếu AC BD
NM // AC (cmt)
NP // BD (cmt)
=> NM NP tại N
Hay
Xét hình thoi MNPQ , ta có : (cmt)
=> hình thoi MNPQ là hình vuông.
tick nha bn

Hình thang ABCD là hình thang cân có hai góc kề một đáy đều bằng 45 0 thì MNPQ là hình vuông.

A M B D Q N C P
a) \(\Delta ABC\)có :
MA = MB ( gt )
NB = NC ( gt )
=> MN là đường trung bình của \(\Delta ABC\)
=> \(MN//AC\)\(;\)\(MN=\frac{1}{2}AC\)
CMTT : \(PQ//AC\)\(;\)\(PQ=\frac{1}{2}AC\)
=> MN // PQ ; MN = PQ .
=> Tứ giác MNPQ là hình bình hành .
b) Theo câu a) , Ta có :
MQ // BD và \(MQ=\frac{1}{2}BD\) ; NP // BD và \(NP=\frac{1}{2}BD\)
+) Hình bình hành MNPQ là hình thoi
=> MN = MQ <=> AC = BD ( Vì \(MN=\frac{1}{2}AC\)\(MQ=\frac{1}{2}BD\))
=> ABCD là hình thang cân .
+) Hình bình hành MNPQ là hình chữ nhật
\(\Rightarrow\) \(\widehat{NMQ}=90^0\)\(\Leftrightarrow\)\(MN\perp MQ\)\(\Leftrightarrow\)\(AC\perp BD\)( Vì MN // AC ; MQ // BD )
=> Hình thang thang ABCD có 2 đường chéo vuông góc với nhau .
+) Hình bình hành MNPQ là hình vuông
\(\Rightarrow\)\(MN=MQ\)\(;\)\(\widehat{NMQ}=90^0\) \(\Leftrightarrow\)\(AC=BC\)và \(AC\perp BD\)
=> ABCD là hình thang cân có 2 đường chéo vuông góc với nhau .

MNPQ là hình thoi vì là hình bình hành có hai cạnh kề bằng nhau.
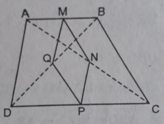
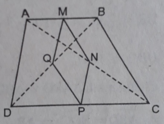
a / hình bình hành
b/ AC=BD ; AB>CD ; AB<AC<CD;AB<BD<CD
c/hình vuông
(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi