Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

kẻ 1 đường thẳng // với 1 đường chéo rồi chứng mình tam giác vuông
Thầy Vũ Tiền Châu , thầy giải thích rõ tí đc k ạ ? E vẽ thử mà nghĩ hoài k ra

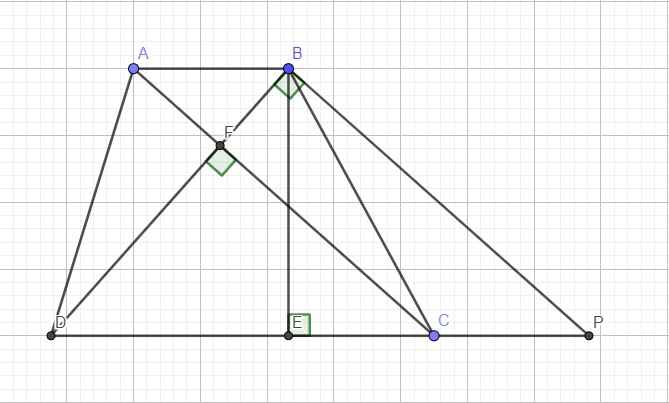
Kẻ đường cao BE \(\Rightarrow BE=12\)
Pitago tam giác vuông BDE:
\(DE=\sqrt{BD^2-BE^2}=9\left(cm\right)\)
Qua B kẻ đường thẳng song song AC cắt CD kéo dài tại P
Do \(AC\perp BD\Rightarrow BP\perp BD\) hay tam giác BPD vuông tại B
Mặt khác \(\left\{{}\begin{matrix}AB||CD\\AC||BP\end{matrix}\right.\) \(\Rightarrow ABPC\) là hbh
\(\Rightarrow AB=CP\Rightarrow AB+CD=CP+CD=DP\)
Hệ thức lượng tam giác vuông BPD:
\(BD^2=DE.DP\Rightarrow DP=\dfrac{BD^2}{DE}=25\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}BE.\left(AB+CD\right)=\dfrac{1}{2}BE.DP=\dfrac{1}{2}.9.25=112,5\left(cm^2\right)\)

Ta áp dụng công thức Brahmagupta để tính
\(s=\frac{\sqrt{\left(AB^2+CD^2+BD^2+AC^2\right)+8\cdot AB\cdot CD\cdot BD\cdot AC-2\left(AB^4+CD^4+BD^4+AC^4\right)}}{4}\)
A) Thay số vào ta đc \(S=6\sqrt{55}\approx44,4972\left(cm^2\right)\)
b) \(S\approx244,1639\left(cm^2\right)\)
hok tốt ...
Công thức Brahmagupta là công thức tính diện tích của một tứ giác nội tiếp (tứ giác mà có thể vẽ một đường tròn đi qua bốn đỉnh của nó) mà hình thang ko có đường tròn nào đi qua đủ bốn đỉnh của nó nên công thức này ko được áp dụng vào bài này

Xét tam giác \(ABD\)vuông tại \(A\):
\(BD^2=AB^2+AD^2\)(định lí Pythagore)
\(=4^2+10^2=116\)
\(\Rightarrow BD=\sqrt{116}=2\sqrt{29}\left(cm\right)\)
Lấy \(E\)thuộc \(CD\)sao cho \(AE\perp AC\)
Suy ra \(ABDE\)là hình bình hành.
\(AE=BD=2\sqrt{29}\left(cm\right),DE=AB=4\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AD\):
\(\frac{1}{AD^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AD^2}-\frac{1}{AE^2}=\frac{1}{100}-\frac{1}{116}=\frac{1}{715}\)
\(\Rightarrow AC=\sqrt{715}\left(cm\right)\)
\(AE^2=ED.EC\Leftrightarrow EC=\frac{AE^2}{ED}=\frac{116}{4}=29\left(cm\right)\)suy ra \(DC=25\left(cm\right)\)
Hạ \(BH\perp CD\).
\(BC^2=HC^2+BH^2=21^2+10^2=541\Rightarrow BC=\sqrt{541}\left(cm\right)\)
\(S_{ABCD}=\left(AB+CD\right)\div2\times AD=\frac{4+25}{2}\times10=145\left(cm^2\right)\)