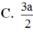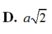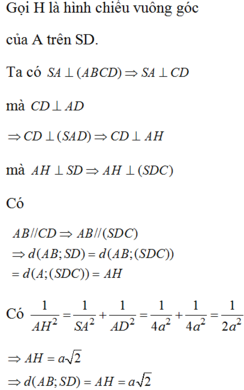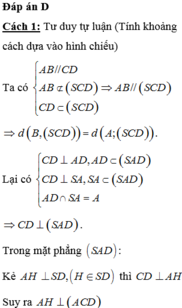Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
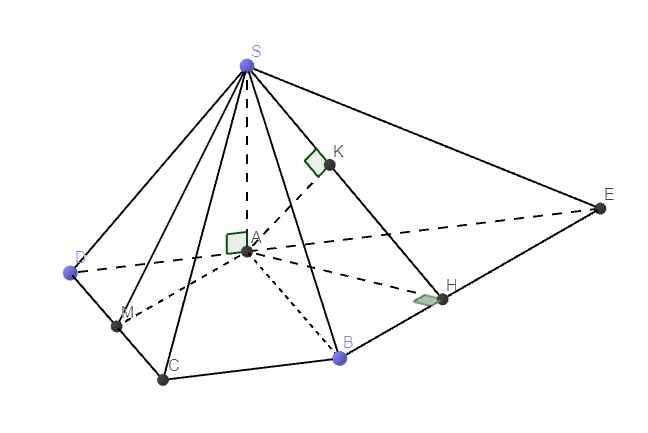
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)

Đáp án là C

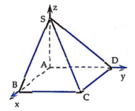
Ta có:
![]()
theo giao tuyến SD.
Trong (SAD) kẻ AH ⊥ DS
![]()
![]()
![]()
Ta có
![]()
Theo bài
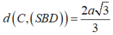

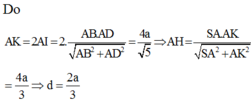
Vì tứ diện SABD có ba cạnh AS, AB, AD đôi một vuông góc nên



Do đó tam giác SAD vuông cân tại A có:
![]()


Chọn D.
Cách 1:

Gọi M là trung điểm của CD, ABMD là hình vuông cạnh bằng 1.
BM= 1 2 DC tam giác BCD vuông cân tại B.
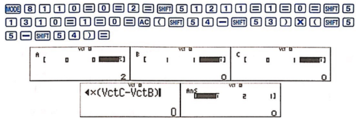
Ta có:
![]()
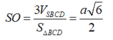
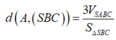
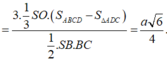
Cách 2: Gọi M là trung điểm của CD, H là trung điểm của BD
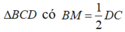
=> Tam giác BCD vuông tại B.
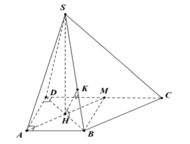
![]()
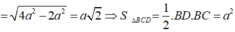
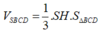
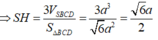
+) Ta có: AH // (SBC)
![]()
![]()
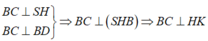
Do đó
![]()
Tam giác SHB có
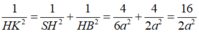
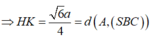

Chọn đáp án D.
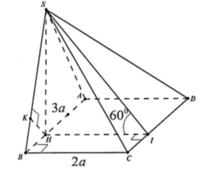
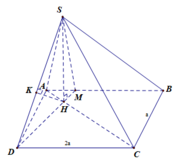
Ta có: ![]()
Kẻ 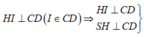
![]()
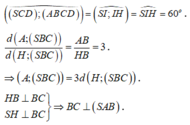
Kẻ ![]()
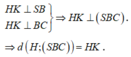
Xét tam giác SHI vuông tại H:
![]()
![]()
Xét tam giác SHB vuông tại B: 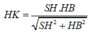
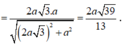
![]()
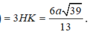

Đáp án C
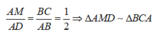
![]()
![]()
⇒ A C ⊥ D M
Vì S H ⊥ ( A B C D ) ⇒ D H ⊥ ( S A C )
từ H kẻ H K ⊥ S D
⇒ H K là khoảng cách cần tính.
Ta có D H H M = D C A M = 4 ⇔ D H D M = 4 5
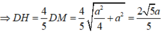
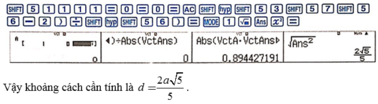
Áp dụng hệ thức lượng trong tam giác vuông.
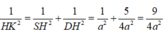
⇒ H K = 2 a 3