Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
b:
Kẻ BH vuông góc AC tại H
(SB;SAC)=(SB;SH)=góc BSH
\(HB=\dfrac{a\cdot a}{a\sqrt{2}}=a\cdot\dfrac{\sqrt{2}}{2}\)
AH=AC/2=a*căn 2/2
=>\(SH=\sqrt{a^2+\dfrac{1}{2}a^2}=a\sqrt{\dfrac{3}{2}}\)
\(SH=\dfrac{a\sqrt{6}}{2};HB=\dfrac{a\sqrt{2}}{2};SB=a\sqrt{2}\)
\(cosBSH=\dfrac{SB^2+SH^2-BH^2}{2\cdot SB\cdot SH}=\dfrac{\sqrt{3}}{2}\)
=>góc BSH=30 độ
c: (SD;(SAB))=(SD;SA)=góc ASD
tan ASD=AD/AS=2
nên góc ASD=63 độ

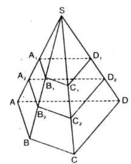
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
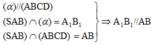
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
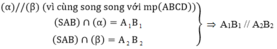
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D

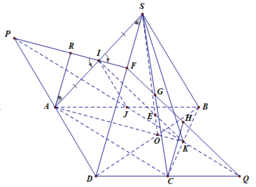
Do M là trung điểm SD, N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN||CD\) (1)
Tương tự PQ là đường trung bình tam giác SAB \(\Rightarrow PQ||AB\)
\(\Rightarrow MN||PQ\Rightarrow\) 4 điểm M, N, P, Q đồng phẳng
Lại có MQ là đường trung bình tam giác SAD \(\Rightarrow MQ||AD\)
Mà \(AD\in\left(ABCD\right)\Rightarrow MQ||\left(ABCD\right)\)
Do \(CD\in\left(ABCD\right)\), từ \(\left(1\right)\Rightarrow MN||\left(ABCD\right)\)
Mà \(\left\{{}\begin{matrix}MN\in\left(MNPQ\right)\\MQ\in\left(MNPQ\right)\\MN\cap MQ=M\end{matrix}\right.\)\(\Rightarrow\left(MNPQ\right)||\left(ABCD\right)\)

Lời giải:
Gọi $Q$ là điểm nằm trên $DC$ sao cho $AD\parallel PQ$
Khi đó: $MN\parallel AD\parallel PQ$ nên $Q\in (MNP)$
$(MNPQ)$ chính là thiết diện của hình chóp cắt bởi $(MNP)$
Giờ ta cần tìm diện tích hình thang $MNPQ$
$SA=SD; DB=SC; AB=CD$ nên $\triangle SAB=\triangle SDC$
Tương ứng ta có $MP=NQ$
$MN=\frac{AD}{2}=\frac{3a}{2}$
$PQ=AD=3a$
$\Rightarrow MNPQ$ là hình thang cân.
Áp dụng định lý cos:
$\cos \widehat{SAB}=\frac{SA^2+AB^2-SB^2}{2SA.AB}=\frac{MA^2+AP^2-MP^2}{2MA.AP}$
$\Leftrightarrow \frac{9a^2+9a^2-27a^2}{2.3a.3a}=\frac{\frac{9}{4}a^2+4a^2-MP^2}{2.\frac{3}{2}a.2a}$
$\Rightarrow MP^2=\frac{37}{4}a^2$
$\Rightarrow h_{MNPQ}=\sqrt{MP^2-(\frac{PQ-MN}{2})^2}=\frac{\sqrt{139}}{4}a$
Diện tích thiết diện:
$S=\frac{MN+PQ}{2}.h=\frac{9\sqrt{139}}{16}a^2$

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)