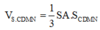Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

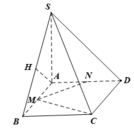
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 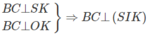
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 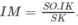
Ta lại có:
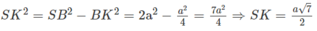
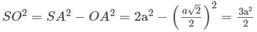
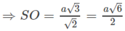
Do đó:
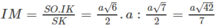
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 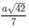

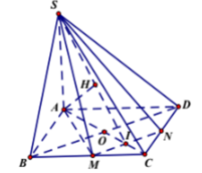
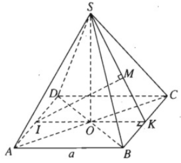
Gọi I = AC ∩ MN ⇒ I là trung điểm của OC, ta có:
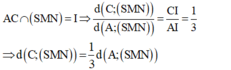
- Ta có: MN// BD mà BD ⊥ (SAC)(cmt) ⇒ MN ⊥ (SAC).
- Trong (SAC) kẻ AH ⊥ SI (H ∈ SI) ⇒ MN ⊥ AH.
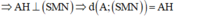
- Ta có:
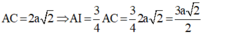
- Xét tam giác vuông SAI ta có:
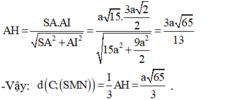


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
E=AB∩CD,G=EN∩SB⇒GE=AB∩CD,G=EN∩SB⇒G là trọng tâm tam giác SAE.
d(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14hd(M,(NCD))=GMGBd(B,(NCD))=12d(B,(NCD))=12.12d(A,(NCD))=14d(A,(NCD))=14h
Tứ diện AEND vuông tại đỉnh A nên 1h2=1AN2+1AE2+1AD2=116a2⇒h=a√66111h2=1AN2+1AE2+1AD2=116a2⇒h=a6611
Vậy d(M,(NCD))=a√6644.d(M,(NCD))=a6644.

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
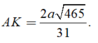

.png)
+ SA⊥(ABCD)⇒SA⊥BDSA⊥(ABCD)⇒SA⊥BD (1)
+ ABCD là hình vuông ⇒AC⊥BD⇒AC⊥BD (2)
+ Từ (1) và (2) suy ra BD⊥(SAC)⇒BD⊥SCBD⊥(SAC)⇒BD⊥SC

Câu hỏi của Phạm Thùy Dương - Toán lớp 11 - Học toán với OnlineMath
Em tham khảo bài làm tại link này nhé!
Cộng đồng học tập online | Học trực tuyến
Lần sau các bài Toán lớp 10, 11, 12 các em đăng trong trang Cộng đồng học tập online | Học trực tuyến nhé! olm hầu như để giải đáp thắc mắc của HỌc sinh tiểu học và trung học em nhé :). Chúc em học tập tốt :)<3


Dựng CH _|_ AB => CH _|_ (SAB)
Giả sử MN cắt AD tại F. Theo định lý Talet ta có:
\(\frac{DF}{MC}=\frac{ND}{NC}=\frac{1}{2}\Rightarrow DF=\frac{MC}{2}=\frac{a}{4}\)
Khi đó \(\frac{PA}{PC}=\frac{AF}{MC}=\frac{5}{2}\Rightarrow\frac{CA}{PA}=\frac{7}{5}\)
Do đó: d (P;(SAB))=\(\frac{5}{7}d\left(C;\left(SAB\right)\right)=\frac{5}{7}CH=\frac{5}{7}\cdot\frac{a\sqrt{3}}{2}=\frac{5a\sqrt{3}}{14}\)