Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

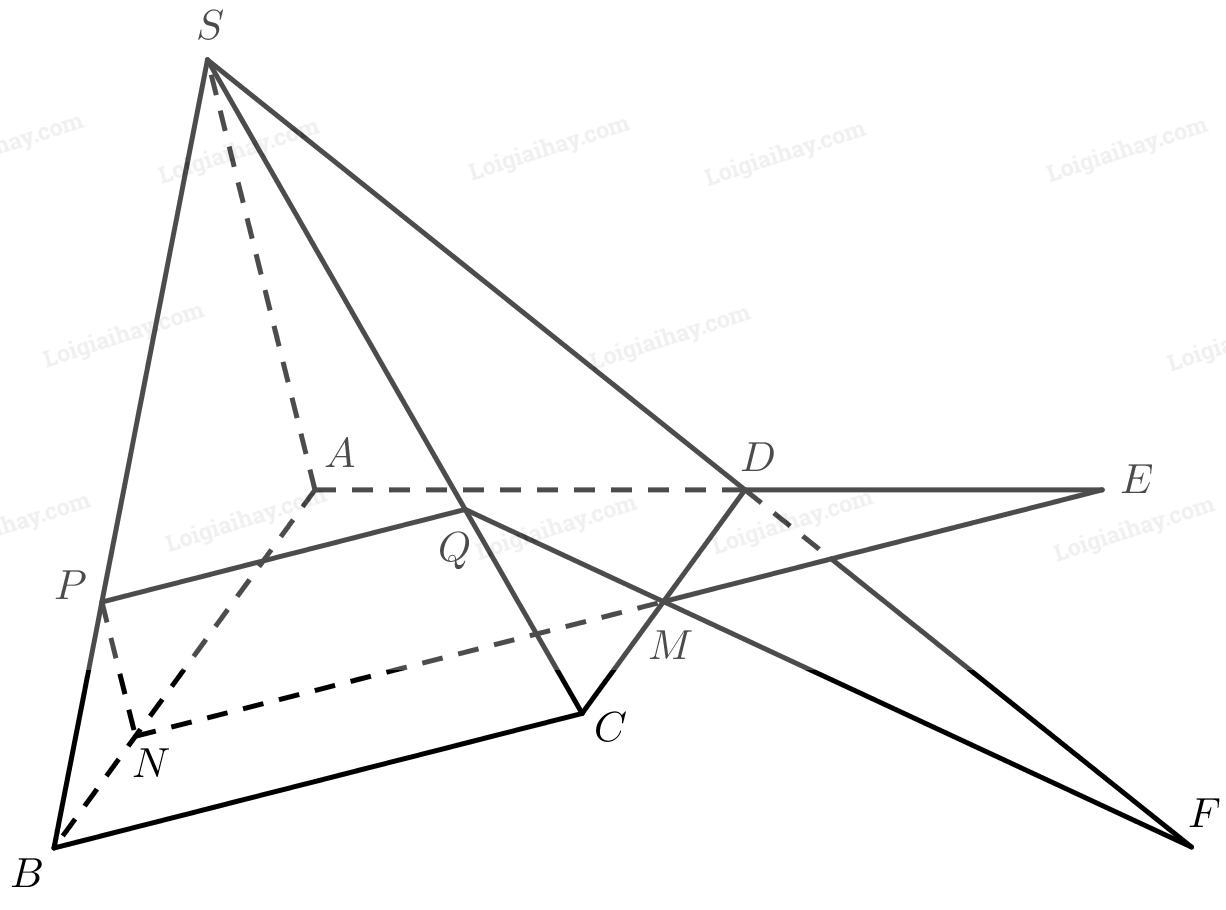
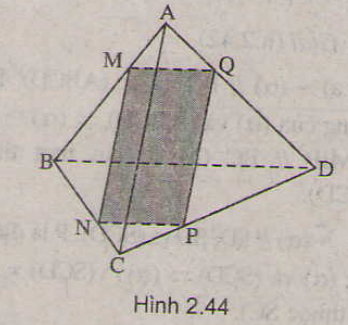
Qua \(M\) dựng đường thẳng song song với \(BC\), cắt \(AB\) tại \(N\).
Qua \(N\) dựng đường thẳng song song với \(SA\), cắt \(SB\) tại \(P\).
Qua \(P\) dựng đường thẳng song song với \(BC\), cắt \(SC\) tại \(Q\).
Vì \(MN\parallel BC,NP\parallel SA\) nên \(\left( {MNPQ} \right) \equiv \left( P \right)\).
Ta có:
\(\begin{array}{l}MN = \left( P \right) \cap \left( {ABC{\rm{D}}} \right)\\NP = \left( P \right) \cap \left( {SAB} \right)\\PQ = \left( P \right) \cap \left( {SBC} \right)\\MQ = \left( P \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Gọi \(E\) là giao điểm của \(A{\rm{D}}\) và \(MN\), \(F\) là giao điểm của \(S{\rm{D}}\) và \(MQ\). Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\E \in MN \subset \left( P \right)\end{array} \right\} \Rightarrow E \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\\left. \begin{array}{l}F \in S{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\\F \in MQ \subset \left( P \right)\end{array} \right\} \Rightarrow F \in \left( P \right) \cap \left( {SA{\rm{D}}} \right)\\ \Rightarrow EF = \left( P \right) \cap \left( {SA{\rm{D}}} \right)\end{array}\)

\(\left(\alpha\right)//SA\) và BC nên \(\left(\alpha\right)//\left(SAD\right)\)
=> MQ //SA, NP//SD ta có
MN//PQ//AD//BC
ABCD : \(\dfrac{BM}{BA}=\dfrac{CN}{CD}\left(1\right)\)
Theo định lí Ta let trong tam giác:
\(\Delta SAB:\dfrac{BM}{BA}=\dfrac{BQ}{BS}=\dfrac{MQ}{SA}\left(2\right)\)
\(\Delta SCD:\dfrac{CN}{CD}=\dfrac{CP}{CS}=\dfrac{PN}{SD}\left(3\right)\)
Từ (1) (2) và (3) suy ra: \(MQ=NP=\dfrac{b-x}{b}a\)
\(PQ=\dfrac{x}{b}.2a\)
\(MN=a+\dfrac{x}{b}a\)
=> thiết diện là hình thang cân và \(S_{td}=\dfrac{1}{2}\left(MN+PQ\right)\sqrt{MQ^2-\left(\dfrac{MN-PQ}{2}\right)^2}\)
= \(\dfrac{1}{2}\left(\dfrac{ab+ax}{b}+\dfrac{2ax}{b}\right)\sqrt{\dfrac{a^2\left(b-x\right)^2}{b^2}-\dfrac{a^2\left(b-x\right)^2}{4b^2}}\)
=\(\dfrac{1}{2}.\dfrac{a\left(b+3x\right)}{b}.\dfrac{a\sqrt{3}\left(b-x\right)}{2b}\)
= \(\dfrac{a^2\sqrt{3}}{12b^2}\left(3x+b\right)\left(3b-3x\right)\le\dfrac{a^2\sqrt{3}}{12b^2}\left(\dfrac{3x+b+3b-3x}{2}\right)^2=\dfrac{a^2\sqrt{3}}{3}\)
Vậy diện tích lớn nhất của thiết diện là \(\dfrac{a^2\sqrt{3}}{3}\) khi x= \(\dfrac{b}{3}\)
[TEX]\frac{QP}{BC}=\frac{SQ}{SB}=\frac{AM}{AB}[/TEX]
\Rightarrow[TEX]QP=\frac{2ax}{b}[/TEX]
[TEX]\frac{QM}{SA}=\frac{BM}{BA}[/TEX]
\Rightarrow[TEX]QM=\frac{a(b-x)}{b}[/TEX]
Do MNPQ là hình thang cân
\Rightarrow[TEX]MN=\frac{a(b-x)}{b}+\frac{2ax}{b}=\frac{ab+ax}{b}[/TEX]
Vậy [TEX]S_{MNPQ}=\frac{(\frac{2ax}{b}+\frac{ab+ax}{b})\frac{\sqrt{3}a(b-x)} {2B}}{2}[/TEX]
=[TEX]\frac{(3ax+ab)(\sqrt{3}ab-\sqrt{3}ax)}{b^2}[/TEX]

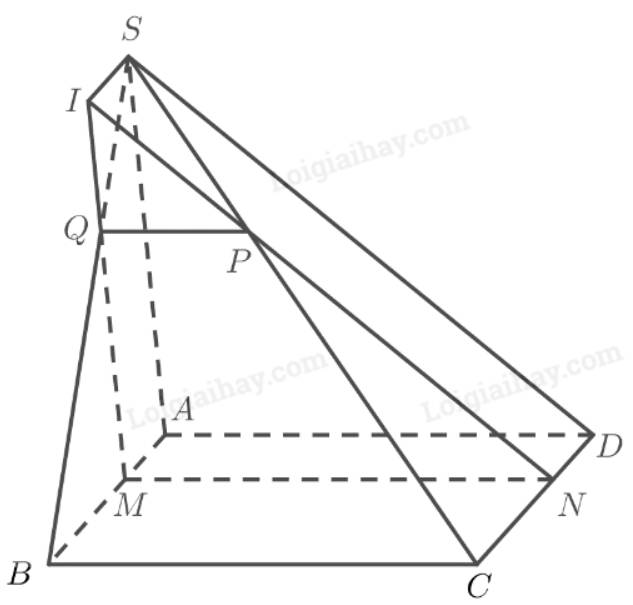
a) Ta có:
\(\left. \begin{array}{l}\left( \alpha \right) \cap \left( {SBC} \right) = PQ\\\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\end{array} \right\} \Rightarrow MN\parallel PQ\parallel BC\)
\( \Rightarrow MNPQ\) là hình thang (1).
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = MQ\\\left( {SA{\rm{D}}} \right) \cap \left( {SAB} \right) = SA\end{array} \right\} \Rightarrow MQ\parallel SA \Rightarrow \frac{{MQ}}{{SA}} = \frac{{BM}}{{AB}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SC{\rm{D}}} \right) = NP\\\left( {SA{\rm{D}}} \right) \cap \left( {SC{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow NP\parallel SD \Rightarrow \frac{{NP}}{{SD}} = \frac{{CN}}{{C{\rm{D}}}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = AD\end{array} \right\} \Rightarrow MN\parallel AD\parallel BC \Rightarrow \frac{{BM}}{{AB}} = \frac{{CN}}{{C{\rm{D}}}}\)
\( \Rightarrow \frac{{MQ}}{{SA}} = \frac{{NP}}{{S{\rm{D}}}}\)
Mà tam giác \(SAD\) đều nên \(SA = S{\rm{D}}\)
\( \Rightarrow MQ = NP\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow MNPQ\) là hình thang cân.
b) Gọi \(I = MQ \cap NP\). Ta có:
\(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {SA{\rm{D}}} \right) = SI\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SC{\rm{D}}} \right) \cap \left( {ABCD} \right) = C{\rm{D}}\end{array} \right\} \Rightarrow SI\parallel AB\parallel C{\rm{D}}\)
\(SI\parallel N{\rm{D}},S{\rm{D}}\parallel NI \Rightarrow SIN{\rm{D}}\) là hình bình hành \( \Rightarrow S{\rm{D}} = NI\)
\(SI\parallel MA,S{\rm{A}}\parallel MI \Rightarrow SIMA\) là hình bình hành \( \Rightarrow S{\rm{A}} = MI\)
Xét tam giác \(IMN\) và tam giác \(SAD\) có: \(MN\parallel A{\rm{D,}}MI\parallel SA,NI\parallel S{\rm{D}},MN = A{\rm{D}}\)
tam giác \(IMN\) là tam giác đều cạnh \(a\).
\(\begin{array}{l}SI\parallel AB \Rightarrow \frac{{SI}}{{BM}} = \frac{{IQ}}{{QM}} \Leftrightarrow \frac{{SI}}{{BM + SI}} = \frac{{IQ}}{{QM + IQ}} \Leftrightarrow \frac{{SI}}{{BM + MA}} = \frac{{IQ}}{{QM + IQ}}\\ \Leftrightarrow \frac{{SI}}{{AB}} = \frac{{IQ}}{{MI}} \Leftrightarrow IQ = \frac{{SI.MI}}{{AB}} = \frac{{x.a}}{a} = x\end{array}\)
\({S_{IMN}} = \frac{{{a^2}\sqrt 3 }}{4},{S_{IPQ}} = \frac{{{x^2}\sqrt 3 }}{4} \Rightarrow {S_{MNPQ}} = {S_{IMN}} - {S_{IPQ}} = \frac{{{a^2}\sqrt 3 }}{4} - \frac{{{x^2}\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{4}\left( {{a^2} - {x^2}} \right)\)