Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáy ABCD là hình gì cạnh a bạn? Hình vuông hay hình thoi?

Bạn coi lại dữ liệu bài toán, vừa thừa vừa thiếu
SA=SC=AC nên tam giác SAC đều thì hiển nhiên \(\widehat{CSA}=60^0\) ko cần đề bài phải cho nữa
\(\widehat{ASB}=90^0\) và SA=SB thì tam giác SAB vuông cân tại S nên ta có \(AB=\sqrt{SA^2+SB^2}=a\sqrt{2}\) cũng không cần đề phải cho
Nhưng hoàn toàn ko có dữ liệu BC hoặc góc A của tam giác ABC để định dạng đáy

Câu 1:
\(ABCI\) là hình vuông \(\Rightarrow\left\{{}\begin{matrix}CD=\sqrt{IC^2+ID^2}=a\sqrt{2}\\AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow AC^2+CD^2=AD^2\Rightarrow\Delta ACD\) vuông cân tạiC
\(\Rightarrow OC\perp CD\) \(\Rightarrow CD\perp\left(SOC\right)\)
Từ O kẻ \(OH\perp SC\Rightarrow OH\perp\left(SCD\right)\) \(\Rightarrow OH\perp SD\)
\(\left\{{}\begin{matrix}BI\perp SO\\BI\perp OC\end{matrix}\right.\) \(\Rightarrow BI\perp\left(SOC\right)\Rightarrow BI\perp OH\)
\(SC=\sqrt{SO^2+OC^2}=a\sqrt{2}\) \(\Rightarrow SH=\frac{SO^2}{SC}=\frac{3a\sqrt{2}}{4}\)
Qua H kẻ đường thẳng song song CD cắt SD tại K
\(\frac{SH}{SC}=\frac{HK}{CD}\Rightarrow HK=\frac{SH.CD}{SC}=\frac{3a}{4}\)
Trên toa OI lấy điểm P sao cho \(OP=\frac{3a}{4}\)
\(\Rightarrow OHKP\) là hình chữ nhật \(\Rightarrow OH//KP\Rightarrow KP\) là đoạn vuông góc chung của \(BI\) và SD
\(\frac{1}{OH^2}=\frac{1}{SO^2}+\frac{1}{OC^2}\Rightarrow KP=OH=\frac{SO.OC}{\sqrt{SO^2+OC^2}}=\frac{a\sqrt{6}}{4}\)
Câu 2:
a/ Kẻ \(MH\perp AC\Rightarrow MH\perp\left(SAC\right)\)
\(\Rightarrow\widehat{MSH}\) là góc giữa SM và (SAC)
\(SM=\sqrt{SA^2+\left(\frac{AB}{2}\right)^2}=a\sqrt{10}\) ; \(MH=\frac{1}{2}\frac{2a\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}\)
\(sin\widehat{MSH}=\frac{MH}{SM}=\frac{\sqrt{30}}{20}\Rightarrow\widehat{MSH}\approx15^053'\)
b/ \(\left\{{}\begin{matrix}MC\perp AB\\MC\perp SA\end{matrix}\right.\) \(\Rightarrow MC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{SMA}\) là góc giữa \(\left(SMC\right)\) và \(\left(ABC\right)\)
\(tan\widehat{SMA}=\frac{SA}{AM}=3\Rightarrow\widehat{SMA}\approx71^033'\)
c/ Gọi N là trung điểm AC \(\Rightarrow NG=\frac{1}{3}NS\) (t/c trọng tâm)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\frac{1}{3}d\left(N;\left(SAB\right)\right)\)
Từ N kẻ \(NK\perp AB\Rightarrow NK\perp\left(SAB\right)\)
\(\Rightarrow NK=d\left(N;\left(SAB\right)\right)\)
\(NK=\frac{1}{2}.\frac{2a\sqrt{3}}{2}=\frac{a\sqrt{3}}{2}\Rightarrow d\left(G;\left(SAB\right)\right)=\frac{a\sqrt{3}}{6}\)

S A B C D H M N K
Kẻ \(AH\perp BD\Rightarrow BD\perp\left(SAH\right)\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và (ABCD)
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AB^2}\Rightarrow AH=\frac{AB.AD}{\sqrt{AB^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
\(SA=\sqrt{SD^2-AD^2}=2a\)
\(tan\widehat{SHA}=\frac{SA}{AH}=\frac{4\sqrt{3}}{3}\Rightarrow\widehat{SHA}\simeq66^035'\)
b/ \(MS=MA\Rightarrow d\left(S;\left(MND\right)\right)=d\left(A;\left(MND\right)\right)\)
Từ A kẻ \(AK\perp MD\Rightarrow AK\perp\left(MND\right)\Rightarrow AK=d\left(A;\left(MND\right)\right)\)
\(AM=\frac{SA}{2}=a\Rightarrow\frac{1}{AK^2}=\frac{1}{AM^2}+\frac{1}{AD^2}\Rightarrow AK=\frac{AM.AD}{\sqrt{AM^2+AD^2}}=\frac{a\sqrt{3}}{2}\)

Gọi O là tâm của hình bình hành ABCD; G = SO∩AM ⇒ G là trọng tâm ΔSAC ⇒ SG/SO = 2/3 ⇒ G cũng là trọng tâm ΔSBD
G ∈ AM ⊂ (P); G ∈ SO ⊂ (SBC) (1)
B' ∈ (P) và B' ∈ SB ⊂(SBC) (2)
D' ∈ (P) và D' ∈ SD ⊂(SBC) (3)
Từ (1); (2); (3) ⇒ G; B'; D' ∈ giao tuyến của (P) và (SBC)
Trong (SBC) vẽ BM//SO//DN (M, N ∈ B'D') ⇒ OG là đường trung bình của hình thang BDNM
⇒ BM + DN = 2OG = SG
Ta có :
x = SB/SB' = (SB' + BB')/SB' = 1 + BB'/SB' = 1 + BM/SG
y = SD/SD' = (SD' + DD')/SD' = 1 + DD'/SD' = 1 + DN/SG
⇒ x + y = 2 + (BM + DN)/SG = 2 + 1 = 3
1/x + 1/y = SB'/SB + SD'/SD = a/b
⇒ 3a/b = (x + y)(1/x + 1/y) ≥ 2√(xy).2√(1/xy) = 4
⇒ u = a/b ≥ 4/3 tối giản ⇒ GTNN của u = 4/3 xảy ra khi x = y ⇔ SB'SB' = SD/SD' ⇔ B'D'//BD

S A B C D H M K O N
a/ \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\)
Mà \(BC\perp AB\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)
\(\left\{{}\begin{matrix}AH\perp BC\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\)
b/ \(\widehat{SBA}=45^0\Rightarrow\Delta SAB\) vuông cân tại A \(\Rightarrow SA=AB=2a\)
Kéo dài MO cắt AB tại N \(\Rightarrow N\) là trung điểm AB \(\Rightarrow MN//BC\Rightarrow MN\perp\left(SAB\right)\)
Do AC cắt (SOM) tại O, mà \(AO=CO\Rightarrow d\left(C;\left(SOM\right)\right)=d\left(A;\left(SOM\right)\right)\)
Từ A kẻ \(AK\perp SN\Rightarrow AK\perp\left(SOM\right)\)
\(\Rightarrow AK=d\left(A;\left(SOM\right)\right)\)
\(\frac{1}{AK^2}=\frac{1}{AN^2}+\frac{1}{SA^2}\Rightarrow AK=\frac{SA.AN}{\sqrt{SA^2+AN^2}}=\frac{2a\sqrt{5}}{5}\)
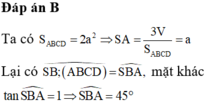
Bạn ghi lại đề, đề bài từ đoạn "gọi M, Q..." trở đi là thấy ko chính xác nữa
Cho hình chóp S.ABCD có ABCD là hình vuông,cạnh a. Hình chiếu vuông góc của S lên ABCD là trung điểm M cạnh AD,SM = a√3/2 . Gọi N,Q là trung điểm của SC,BC.Xác định và tính cosin của góc tạo bởi mp ADN và mp SBC