Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

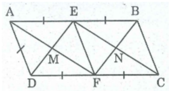
* Xét tứ giác AEFD, ta có:
AB // CD (gt) hay AE // FD
AE = 1/2 AB (gt)
FD = 1/2 CD (gt)
Suy ra: AE = FD
Tứ giác AEFD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
AD = AE = 1/2 AB . Vậy tứ giác AEFD là hình thoi.
* Xét tứ giác AECF, ta có: AE // CF (gt)
AE = 1/2 AB (gt)
CF = 1/2 CD (gt)
Suy ra: AE = CF
Tứ giác AECF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

A D F M E B C N
a) Tứ giác AEFD là hình thoi, tứ giác AECF là hình bình hành (tự chứng minh).
b) Tứ giác AECF là hình bình hành nên EN // FM. Tứ giác AECF là hình bình hành nên EM // FN. AEFD là hình thoi nên AF \(\perp\) DE.
Hình bình hành EMFN có \(\widehat{M}=90^o\) nên là hình chữ nhật.
c) Hình chữ nhật EMFN là hình vuông
\(\Leftrightarrow\) ME = MF \(\Leftrightarrow\) DE = AF (vì DE = 2ME, AF = 2MF)
\(\Leftrightarrow\) Hình thoi AEFD có hai đường chéo bằng nhau
\(\Leftrightarrow\) AEFD là hình vuông \(\Leftrightarrow\) \(\widehat{A}=90^o\).
\(\Leftrightarrow\) Hình bình hành ABCD là hình chữ nhật.
Như vậy, hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật.

a) bạn tự vẽ hình nhé!
Có : \(AE=BE=\frac{1}{2}AB\) (đề cho)
\(DF=CF=\frac{1}{2}DC\) (đề cho)
mà \(AB=CD\)
\(\Rightarrow\) \(AE=BE=DF=CF\)
Xét tứ giác AEFD có:
\(AE=DF\) (cmt) và AE//DF( AB//CD)
\(\Rightarrow\) Tứ giác AEFD là hình bình hành
Xét tứ giác AECF có :
AE = CF ( cmt) và AE//CF ( AB//CD)
\(\Rightarrow\) Tứ giác AECF là hình bình hành
M là giao điểm của AF và DE
\(\Rightarrow\) AM = FM=\(\frac{1}{2}AF\) ( tính chất đ/chéo hbhành) (1)
N là giao điểm của BF và CE
\(\Rightarrow\) EN = CN=\(\frac{1}{2}CE\) ( tính chất đ/chéo hbhành) (2)
Có AF = AM + FM
CE = EN + CN
mà AE = CE ( AECF là hbh)
Từ (1) và (2) suy ra MF= EN và MF//EN ( AF//CE )
\(\Rightarrow\) EMFN là hình bình hành (3)
Có AE = AD ( cùng bằng 2AB ) và AEFD là hình bình hành nên AEFD là hình thoi
\(\Rightarrow\) AF \(\perp\) DE tại M hay góc EMF = 90 độ (4)
Từ (3) và (4) suy ra : EMFN là hcn

b tham khảo nha
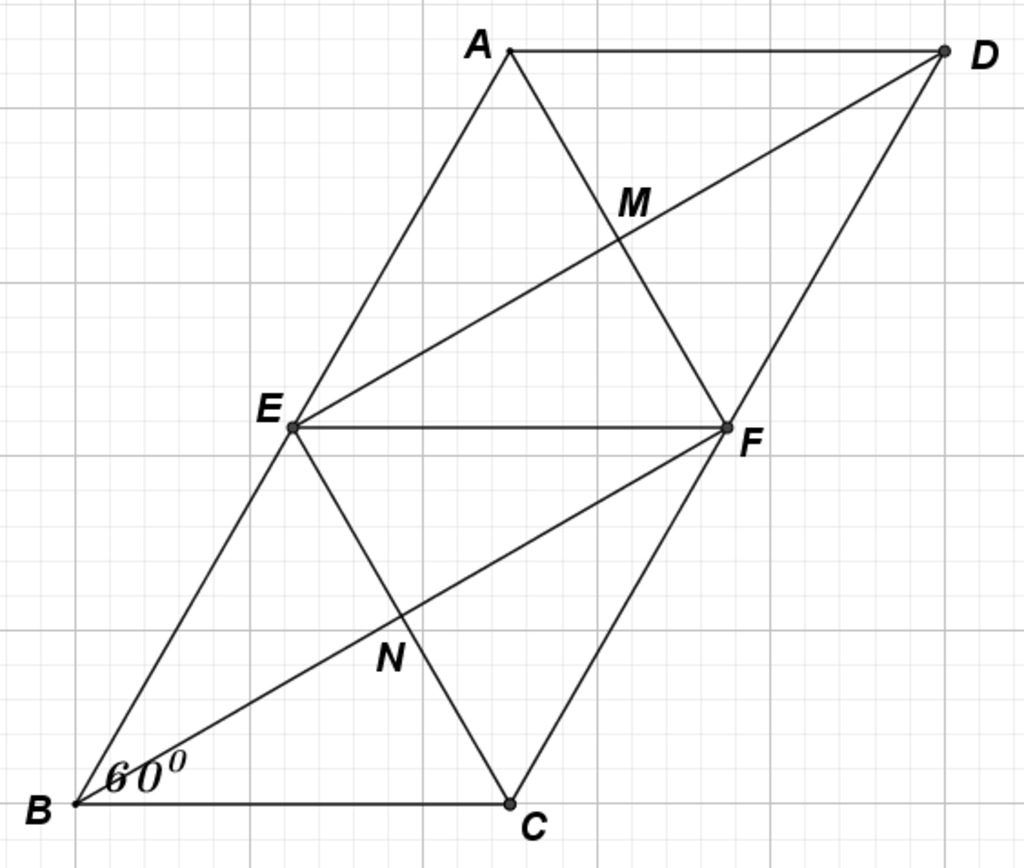
a) Do ABCD là hình bình hành nên AB= CD và AB//CD
Và E và F là trung điểm của AB và CD => AE=BE=CF=DF và BE//DF
Xét tứ giác DEBF có : BE//DF và BE=DF=> DEBF là hình bình hành
b)
Xét AEDF có AE//DF và AE=DF=> AEDF là hình bình hành
Lại có: CD= 2BC= 2 AD nên AD= AE (=1/2 CD)
=> hình bình hành AEDF là hình thoi
c)ta cm được AECF là hình bình hành và M, N là trung điểm của AF và CE
=> MF= EN và MF//EN=> EMFN là hình bình hành
Lại có AEDF là hình thoi nên AN⊥DE tại M
=> góc EMF vuông=> hình bình hành EMFN là hình chữ nhật
d) Chứng minh được
SAFB=12SABCDSBEC=14SABCDˆB=600⇒ΔBECdeucanh=AB2=2(cm)⇒SBEC=√3(cm2)⇒SAFB

Các bạn giúp mik vs ạ! Xin các bạn đấy
Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi