K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 4 2017
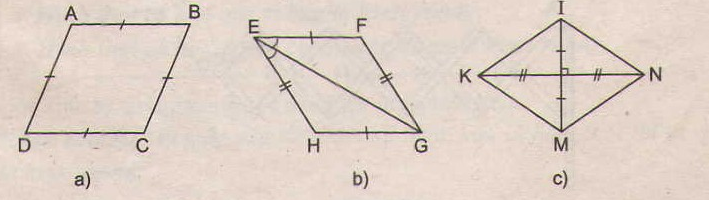
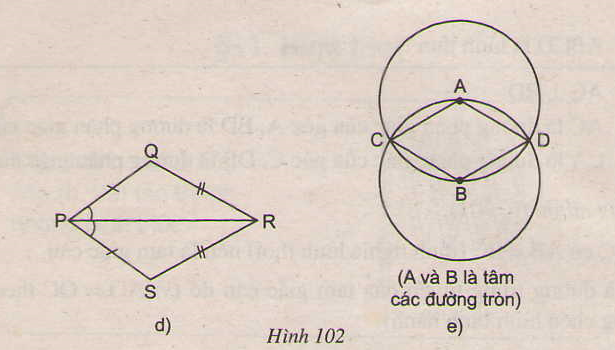
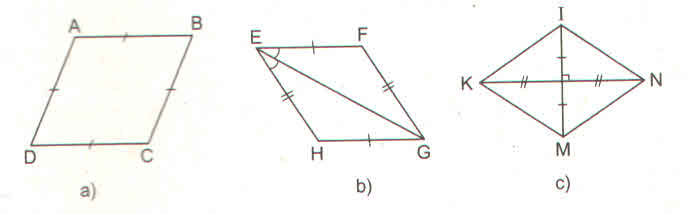
73. Tìm các hình thoi trên hình 102.
Bài giải:
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
21 tháng 4 2017
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
SG
1
SG
2
10 tháng 5 2017
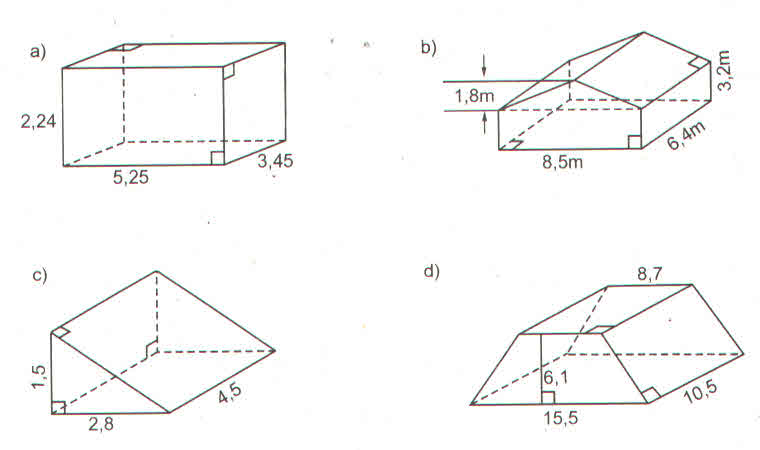
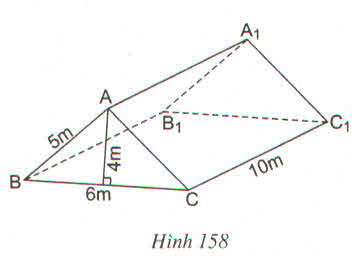
Diện tích đáy ABC: S1= 1/2.6.4=12 (m2)
Diện tích mặt BCC1B1: S2=6.10=60 (m2)
Diện tích AA1C1C: S3= 10.5=50 (m2)
Ta thấy hai mặt AA1B1B và AA1C1C bằng nhau nên:
Stp= 2S1+S2+2S3= 2.12+60+2.50= 184 (m2)
SG
3
30 tháng 6 2017
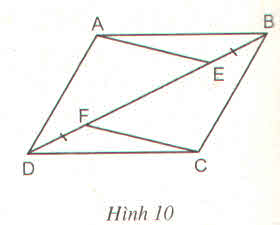
Gọi O là giao điểm của AC và BD. Ta có OA = OC, OE = OF nên AECF là hình bình hành. Suy ra AE // CF.
10 tháng 5 2017
| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| h | 8 | 18 | 17 | 24 | 13 |
| Diện tích 1 đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |
SG
1
NL
24 tháng 4 2017
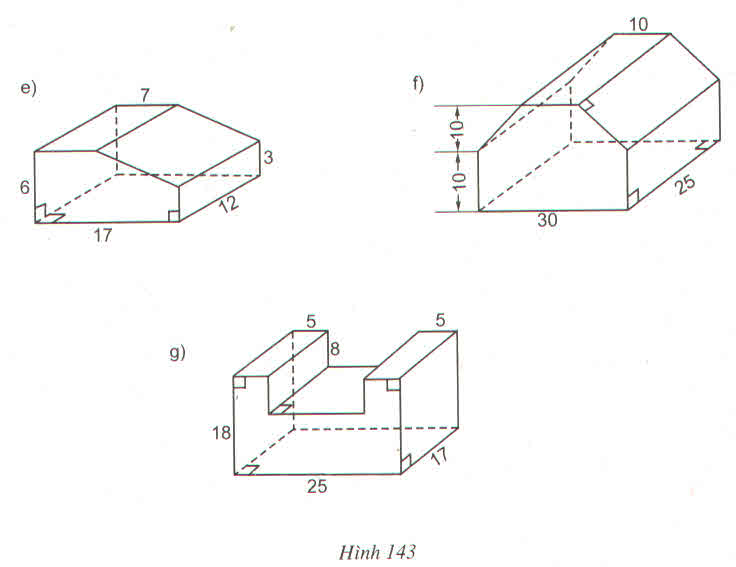
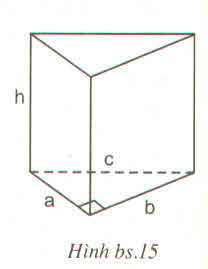
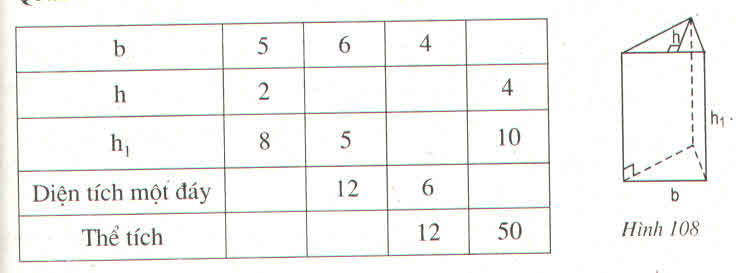
Ta có : Diện tích đáy : S = b.h
Thể tích V = S.h1
+ Ở cột 2 : S = b.h =
. 5.2 = 5
V = S .h1 = 5. 8 = 40
+ Ở cột 3 : S =. b.h => h =
=
= 4
V = S .h1 = 12.5 = 60
+ Ở cột 4: h = =
= 3
V = S .h1 =>h1 = =
= 2
+ Ở cột 5: V = S .h1 =>h1 = =
= 5
S = b.h = b =
=
=
Vậy có kết quả sau khi điền vào bảng sau là:
|
b(cm) |
5 |
6 |
4 |
5 |
|
h(cm) |
2 |
4 |
3 |
4 |
|
h1(cm) |
8 |
5 |
2 |
10 |
|
Diện tích một đáy(cm) |
5 |
12 |
6 |
|
|
thể tích |
40 |
60 |
12 |
50 |
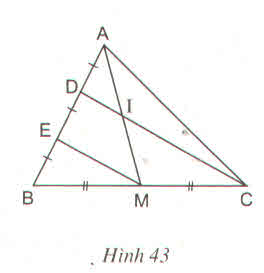
∆BDC có BE = ED và BM = MC
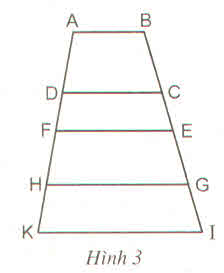
nên EM // DC
==> DI // EM
∆AEM có AD = DE và DI // EM
==> AI = IM.
Trong tam giác BAC có: EM là ĐTB nên DC // EM
ta có: I ∈ DC => DI // EM (DC // EM)
=> I là TĐ của AM nên AI = IM