Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình you tự vẽ nha
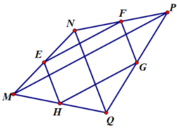
a) Xét tam giác MKG = tam giác NHG ( c-g-c)
=> KG = HG
CMTT ta có KG = KI, KI = IH, HI = HG
Từ đây suy ra KG = KI = IH = HG
=> tứ giác GHIK là hình thoi
b) Vì GHIK là hình thoi => nó cx đồng thời là hình thang
Dễ thấy KH là đường trung bình trong hình thang
=> \(KH=\dfrac{MN+PQ}{2}=\dfrac{10+10}{2}=10\left(cm\right)\)
CMTT ta có \(GI=6\left(cm\right)\)
Ta có : \(S_{GHIK}=\dfrac{KH\cdot GI}{2}=\dfrac{10\cdot6}{2}=30\left(cm^2\right)\)

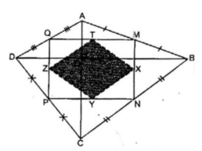
Kẻ đường chéo MP và NQ
Trong △ MNP ta có:
X là trung điểm của MN
Y là trung điểm của NP
nên XY là đường trung bình của △ MNP
⇒ XY // MP và XY = 1/2 MP (tính chất đường trung bình của tam giác) (3)
Trong △ QMP ta có:
T là trung điểm của QM
Z là trung điểm của QP
nên TZ là đường trung bình của △ QMP
⇒ TZ // MP và TZ = 1/2 MP (tính chất đường trung bình của tam giác) (4)
Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.
Trong △ MNQ ta có XT là đường trung bình
⇒ XT = 1/2 QN (tính chất đường trung bình của tam giác)
Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ
Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi
S X Y Z T = 1/2 XZ. TY
mà XZ = MQ = 1/2 BD = 1/2. 8 = 4 (cm);
TY = MN = 1/2 AC = 1/2 .6 =3 (cm)
Vậy : S X Y Z T = 1/2. 3. 4 = 6( c m 2 )








Mơn bạn nhìu