Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
nên ABEC là hình bình hành
b: ABEC là hình bình hành
=>AC//BE và AC=BE
AC=BE
AC=AD
Do đó: BE=AD
AC//BE
=>BE//AD
Xét tứ giác ADBE có
AD//BE
AD=BE
Do đó: ADBE là hình bình hành
c: ADBE là hình bình hành
=>AB cắt DE tại trung điểm của mỗi đường
=>N là trung điểm chung của AB và DE
=>NA=NB
d: Xét ΔBAC có BM/BC=BN/BA
nên MN//AC
MN//AC
AC\(\perp\)AB
Do đó: MN\(\perp AB\)

bài 1 hình tự vẽ
ABCD là hcn nên góc B=90
áp dụng pytago => BC=6cm
bài 2 hình lười vẽ => tự vẽ hình
tam giác ABC có d tđ AB, e tđ BC
=> DE là đtb
=> DE // và = 1/2 AC (1)
mà M là trung điểm AC => AM = 1/2 AC (2)
(1) và (2) => DE // và = AM
=> ĐPCM
câu b
có câu a mà để ADEM là hcn thì => góc A=90 độ
<=> tam giác ABC vuông tại A
câu c hình như sai, M di chuyển trên BC, M là tđ của BC rồi mà
bài 3
câu a cm tam giác oab cân O
=> oa=ob
cmtt => oa=oc
=> DPCM
câu b
tam giác oab cân o có ox là đường cao
=> góc aox = góc xob
cmtt => góc aoy= góc yoc
tổng 4 góc đó = góc boc
mà góc xoa + góc aoy =90
=> ...
=> góc boc = 180 độ
=> ĐPcm
bài 4
câu a
admn là hcn ( vì có 3 góc vuông)
câu b
cm dn là đtb
=> n là tđ Ac
có ..
=> adce là hbh
mà ac vuông góc de
=> adce là hình thoi
câu c :V, cm ở câu b rồi kìa
câu d, ko biết cách trình bày nhưng để diều đó xảy ra khi tam giác abc cân tại a
vì bài làm hơi dài nên tôi làm hình như hơi quá tắt thì phải, cái chỗ chám chấm ko hiểu thì nói tôi chỉ cho
ở chỗ bài 3
góc box + góc xoa + góc aoy + góc yoc = góc boc
mà góc box = góc xoa và góc aoy = góc yoc
=> 2 ( góc xoa + góc aoy) = góc boc
mà góc xoa + góc aoy = 90
=> 2( góc xoa + góc aoy) = 90 * 2 = góc boc = 180
=> ĐPCM
câu b bài 4
tự cm dn là đường trung bình của tam giác abc
=> n là trung điểm ac
có d đối xứng với e qua n => n là trung điểm de
=> adce là hbh
chỉ vậy thôi nhá

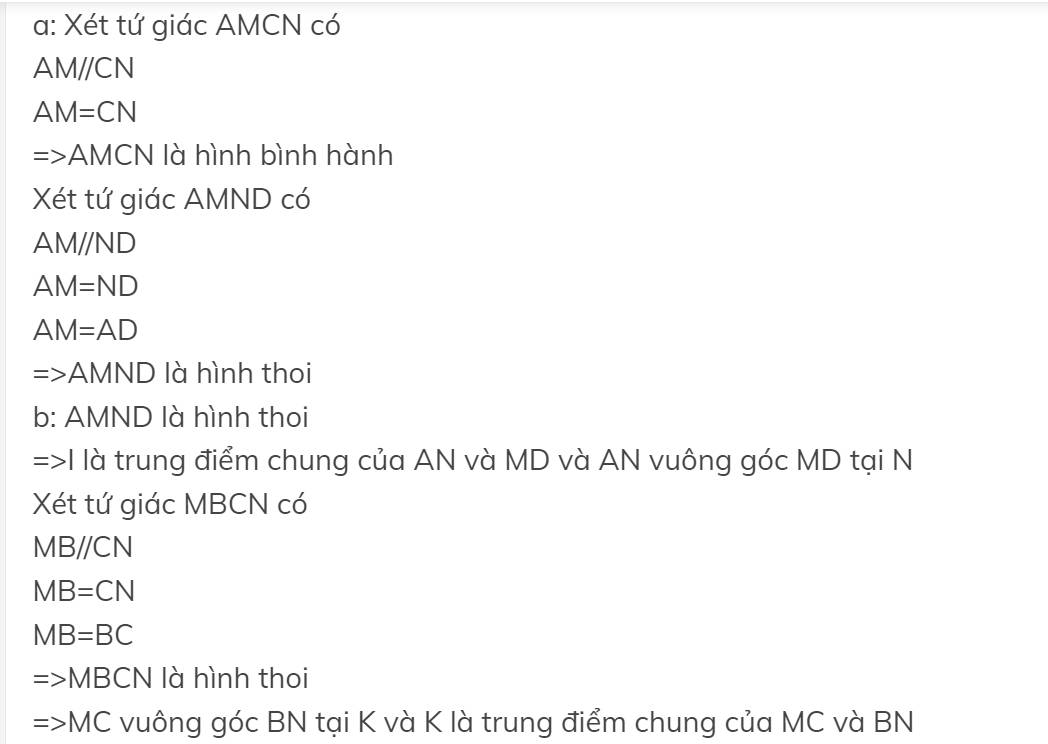
a: Xét tứ giác AMCN có
AM//CN
AM=CN
=>AMCN là hình bình hành
Xét tứ giác AMND có
AM//ND
AM=ND
AM=AD
=>AMND là hình thoi
b: AMND là hình thoi
=>I là trung điểm chung của AN và MD và AN vuông góc MD tại N
Xét tứ giác MBCN có
MB//CN
MB=CN
MB=BC
=>MBCN là hình thoi
=>MC vuông góc BN tại K và K là trung điểm chung của MC và BN
Xét ΔMDC có
MN là trung tuyến
MN=DC/2
=>ΔMDC vuông tại M
Xét tứ giác MINK có
góc MIN=góc MKN=góc IMK=90 độ
=>MINK là hình chữ nhật
c: Xét ΔMDC có MI/MD=MK/MC
nên IK//DC

Bài 3:
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi
b: Xét tứ giác BEFC có
BE//CF
BE=CF
Do đó: BEFC là hình bình hành
mà BE=BC
nên BEFC là hình thoi
Xét ΔEDC có
EF là đường trung tuyến
EF=DC/2
Do đó: ΔEDC vuông tại E
Xét tứ giác EMFN có
\(\widehat{EMF}=\widehat{ENF}=\widehat{MEN}=90^0\)
Do đó: EMFN là hình chữ nhật
c: Để EMFN là hình chữ nhật thì EM=FN
=>ED=AF
=>AEFD là hình vuông
=>\(\widehat{BAD}=90^0\)

Ta có: AM=MB=AB/2 ( M là trung điểm AB)
DN=NC=DC/2 (N là trung điểm DC)
Mà: AB=AC (ABCD LÀ HBH)
=> AM=MB=DN=NC
Xét tứ giác AMCN:
AM=NC (cmt)
AM//NC (AB//CD)
Vậy AMCN là hình bình hành
b.
Xét tứ giác AMND:
AM=ND (cmt)
AM//ND (AB//CD)
Vậy AMDN là hình bình hành
C. hình như bạn chép sai đề rồi: TK??



a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Hình bình hành AMND có AM=AD(\(=\dfrac{AB}{2}\))
nên AMND là hình thoi
Xét tứ giác BMNC có
BM//NC
BM=NC
Do đó: BMNC là hình bình hành
Xét hình bình hành BMNC có \(MB=BC\left(=\dfrac{AB}{2}\right)\)
nên BMNC là hình thoi
b:
AMND là hình thoi
=>\(MN=AD=\dfrac{DC}{2}\)
Xét ΔDMC có
MN là đường trung tuyến
\(MN=\dfrac{DC}{2}\)
Do đó: ΔDMC vuông tại M
=>\(\widehat{DMC}=90^0\)
c: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AN//CM
cảm ơn nha