Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 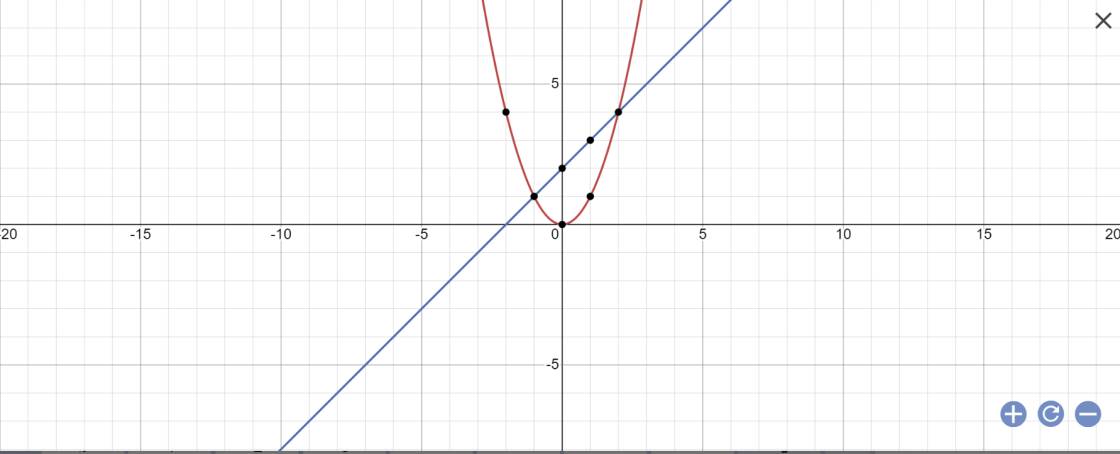
b: PTHĐGĐ là:
x^2-x-2=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1

Bài 1:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x-3=x-1\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)

b: PTHĐGĐ là:
x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1
=>y=16 hoặc y=1

a: 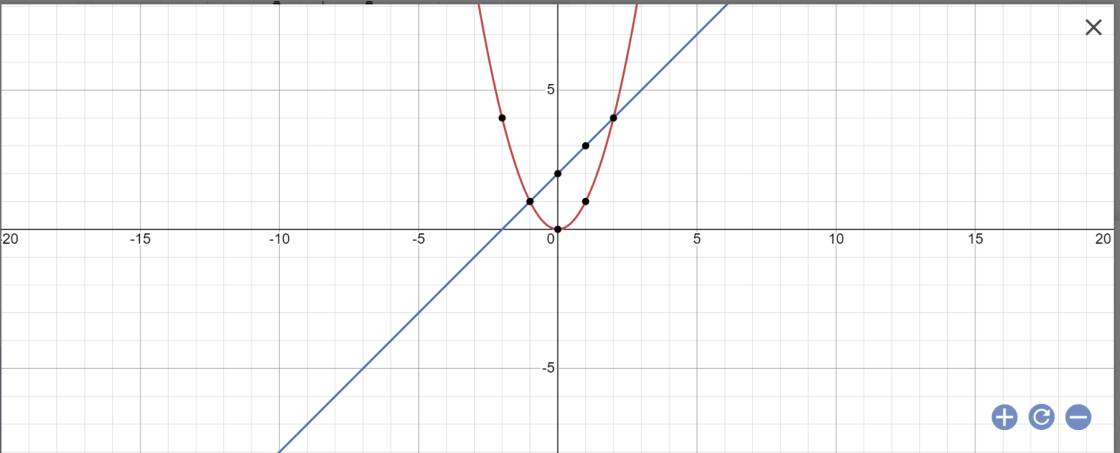
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0

a)Tự vẽ
b) Xét pt hoành độ gđ của (P) và (d) có:
\(\dfrac{3}{2}x^2=x+\dfrac{1}{2}\)
\(\Leftrightarrow3x^2-2x-1=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\Rightarrow y=\dfrac{3}{2}.\left(-\dfrac{1}{3}\right)^2=\dfrac{1}{6}\\x=1\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
Vậy gđ của (d) và (P) là \(\left(-\dfrac{1}{3};\dfrac{1}{6}\right),\left(1;\dfrac{3}{2}\right)\)
c) Gọi đt cần tìm có dạng (d') \(y=ax+b\) (a2+b2>0)
Gọi A(-4;y1) và B(2;y2) là hai giao điểm của (P) và (d')
\(A;B\in\left(P\right)\Rightarrow\left\{{}\begin{matrix}y_1=24\\y_2=6\end{matrix}\right.\)
\(\Rightarrow A\left(-4;24\right),B\left(2;6\right)\) \(\in\left(d'\right)\)
\(\Rightarrow\left\{{}\begin{matrix}24=-4a+b\\6=2a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=12\end{matrix}\right.\) (thỏa)
Vậy (d'): y=-3x+12

b. PTHDGD: \(2x=x+1\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\)
Vậy tọa độ giao điểm 2 đt là \(A\left(1;2\right)\)




b: Vì a=1=a' nên (d)//(d')