Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có
![]() .
.
![]() .
.
Hình bên dưới là đồ thị của hàm số ![]() và
và ![]() .
.
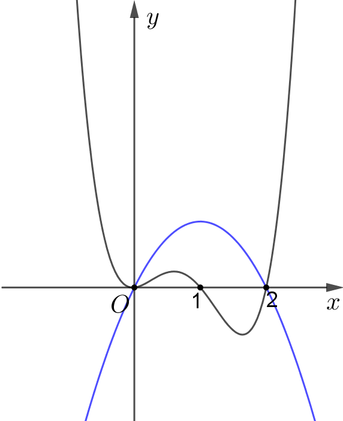
Dựa vào hình vẽ ta thấy đồ thị hàm số ![]() và
và ![]() cắt nhau tại 2 điểm phân biệt, đồng thời
cắt nhau tại 2 điểm phân biệt, đồng thời ![]() khi
khi ![]() hoặc
hoặc ![]() ,
, ![]() khi
khi ![]() .
.
Do đó ![]() đổi dấu qua
đổi dấu qua ![]() ,
, ![]() .
.
Vậy hàm số g(x) có hai điểm cực trị.

Chọn D
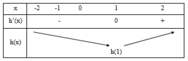
Trong khoảng ![]() đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)

Chọn B
Ta có g’(x) = f’(x) + 1.
Đồ thị của hàm số y= g’(x) là phép tịnh tiến đồ thị của hàm số y= f’(x) theo phương song song với Oy lên trên 1 đơn vị.
Khi đó đồ thị hàm số y= g’(x) cắt trục hoành tại hai điểm phân biệt.
=> Hàm số y= g(x) có 2 điểm cực trị.

Ta có ![]()
Suy ra đồ thị của hàm số g’ (x) là phép tịnh tiến đồ thị hàm số y= f’ (x) theo phương Oy xuống dưới ![]() đơn vị.
đơn vị.
Ta có ![]() và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
Chọn D.

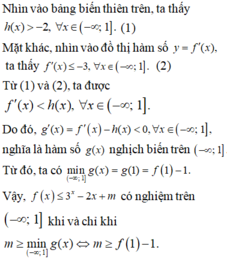
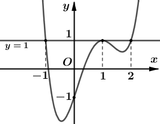
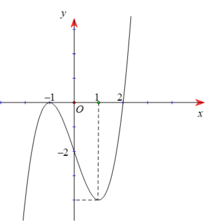

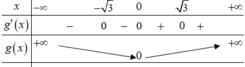

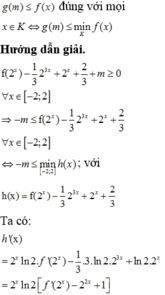
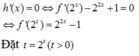
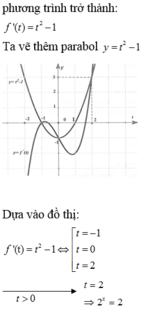


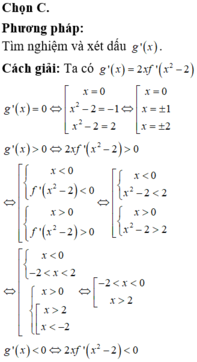

\(g’\left( x \right) = \left( {3{x^2} + 1} \right)f’\left( {{x^3} + x – 1} \right)\)
Xét \(g’\left( x \right) = 0 \Leftrightarrow f’\left( {{x^3} + x – 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^3} + x – 1 = – 1\\{x^3} + x – 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} + x = 0\\{x^3} + x – 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).
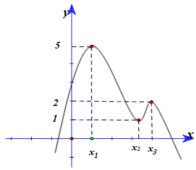
\(\begin{array}{l}g\left( 0 \right) = f\left( { – 1} \right) + m = 3 + m\\g\left( 1 \right) = f\left( 1 \right) + m = – 1 + m\end{array}\)
\(\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right)\\ \Rightarrow 3 + m = – 10\\ \Leftrightarrow m = – 13\end{array}\)