Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Vậy: M(-1;1) và N(2;4)
Gọi (d):y=ax+b là ptđt đi qua hai điểm M và N
\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-3\\-a+b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
Vậy: (d): y=x+2

\(a,\Leftrightarrow1+m=-2\Leftrightarrow m=-3\\ \Leftrightarrow y=x-3\\ \text{Thay }x=2;y=5\Leftrightarrow5=2-3=-1\left(\text{vô lí}\right)\\ \Leftrightarrow E\notinđths\\ b,\text{PT giao Ox và Oy: }\left\{{}\begin{matrix}y=0\Rightarrow x=-m\Rightarrow E\left(-m;0\right)\Rightarrow OE=\left|m\right|\\x=0\Rightarrow y=m\Rightarrow F\left(0;m\right)\Rightarrow OF=\left|m\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến EF
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OE^2}+\dfrac{1}{OF^2}=\dfrac{1}{2m^2}=\dfrac{1}{3^2}=\dfrac{1}{9}\)
\(\Leftrightarrow m^2=\dfrac{9}{2}\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{\sqrt{2}}\\m=-\dfrac{3}{\sqrt{2}}\end{matrix}\right.\)

a: 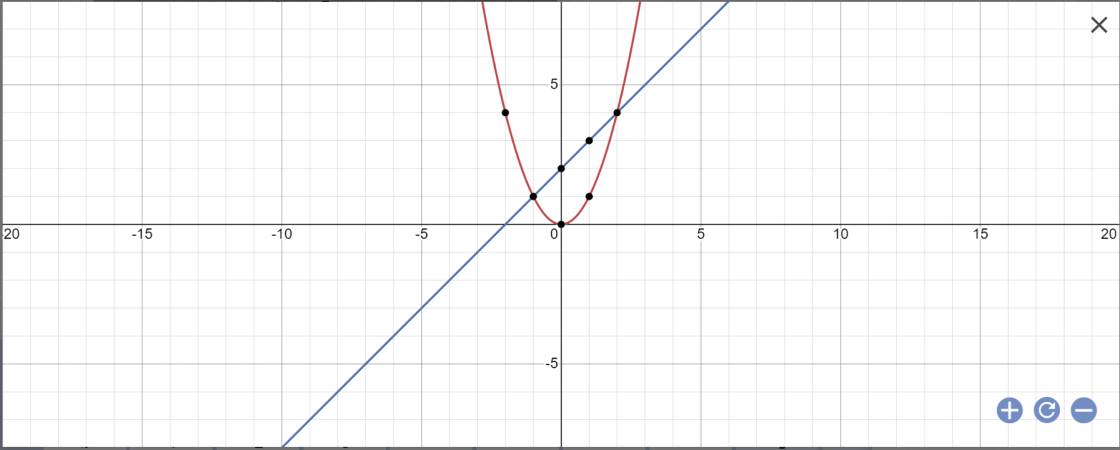
PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
Khi x=-1 thì y=(-1)^2=1
Khi x=2 thì y=2^2=4
b: Để y=(m-1)x+m+n trùng với y=-2x+1 thì
m-1=-2 và m+n=1
=>m=-1 và n=1-m=1-(-1)=2

Lời giải:
a) $y_M=\frac{-x_M^2}{2}=\frac{-(-3)^2}{2}=\frac{-9}{2}$
Đường thẳng $OM$ có dạng: $y=ax$
$\Rightarrow y_M=ax_M\Leftrightarrow \frac{-9}{2}=a.(-3)$
$\Rightarrow a=\frac{3}{2}$
Vậy ĐT $OM$ là: $y=\frac{3}{2}x$
b) Gọi PTĐT $CE$ có dạng $y=ax+b$
PT hoành độ giao điểm giữa $(P)$ và $CE$ là:
$\frac{-x^2}{2}-ax-b=0$
$\Leftrightarrow x^2+2ax+2b=0(*)$
$(P)$ và $CE$ cắt nhau tại 2 điểm có hoành độ $-1;2$ nghĩa là PT $(*)$ nhân $x=-1$ và $x=2$ là nghiệm
\(\Rightarrow \left\{\begin{matrix} 1-2a+2b=0\\ 4+4a+2b=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{-1}{2}\\ b=-1\end{matrix}\right.\)
Vậy PTĐT $CE$ có dạng $y=-\frac{1}{2}x-1$
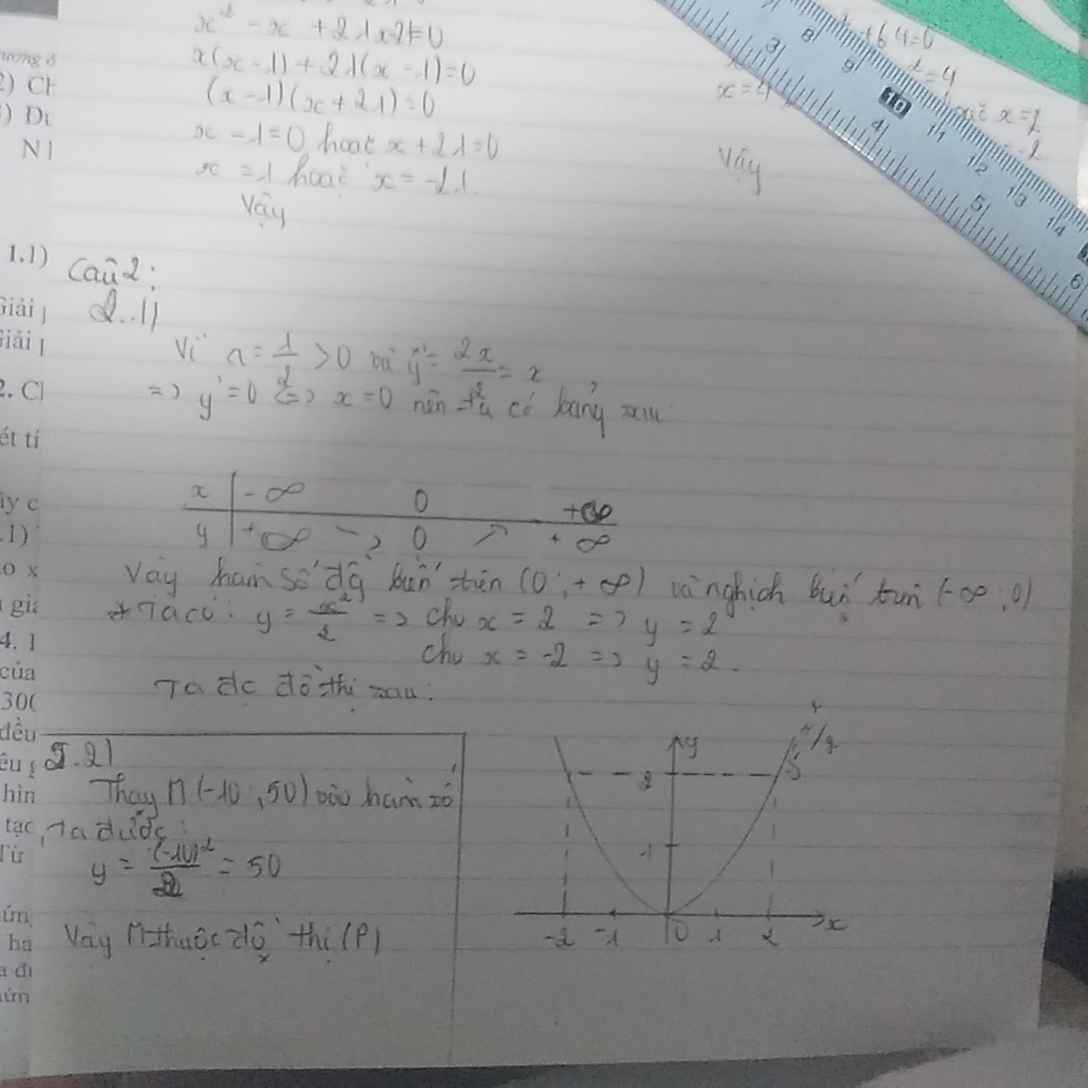
M thuộc (P) thì 1/2*(-10)^2=50