Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cos x\) là hàm số chẵn.
b)
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\cos x\) | \( - 1\) | \( - \frac{{\sqrt 2 }}{2}\) | \(0\) | \(\frac{{\sqrt 2 }}{2}\) | 1 | \(\frac{{\sqrt 2 }}{2}\) | 0 | \( - \frac{{\sqrt 2 }}{2}\) | \( - 1\) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cos x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right),\;k\; \in \;\mathbb{Z}\)

Đặc điểm nào sau đây Không Phải của đường sức điện trường đều?
A. Các đường sức song song cùng chiều
| B. Các đường sức song song ngược chiều | |||
|

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) = - \cot x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cot x\) là hàm số lẻ.
b)
\(x\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(\cot x\) | \(\sqrt 3 \) | \(1\) | \(\frac{{\sqrt 3 }}{3}\) | \(0\) | \( - \frac{{\sqrt 3 }}{3}\) | \( - 1\) | \( - \sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).

a)
x | \( - \pi \) | \( - \frac{{5\pi }}{6}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{6}\) | 0 | \(\frac{\pi }{6}\) | \(\frac{\pi }{2}\) | \(\frac{{5\pi }}{6}\) | \(\pi \) |
\(y = \sin x\) | 0 | \( - \frac{1}{2}\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 |
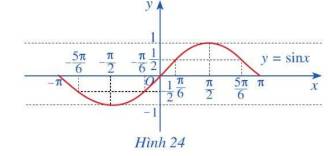
b) Trong mặt phẳng Oxy, hãy biểu diễn các điểm \(\left( {x;y} \right)\) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) với nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\)(Hình 24).
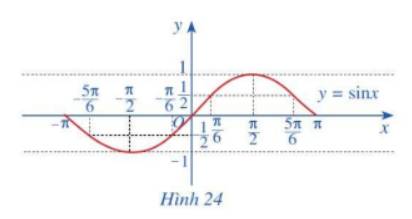
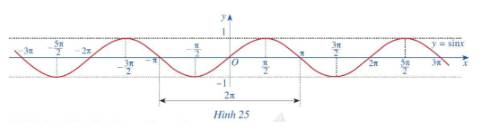
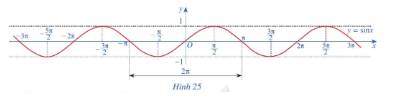
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \sin x\)trên R được biểu diễn ở Hình 25.

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \tan \left( { - x} \right) = - \tan x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \tan x\) là hàm số lẻ.
b)
\(x\) | \( - \frac{\pi }{3}\) | \( - \frac{\pi }{4}\) | \( - \frac{\pi }{6}\) | \(0\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) |
\(\tan x\) | \( - \sqrt 3 \) | \( - 1\) | \( - \frac{{\sqrt 3 }}{3}\) | \(0\) | \(\frac{{\sqrt 3 }}{3}\) | \(1\) | \(\sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).






 . Tính
. Tính 

 .
. . Tính
. Tính  bằng:
bằng:
 bằng:
bằng:

 .
.

a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) = - \sin x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \sin x\) là hàm số lẻ.
b)
\(x\)
\( - \pi \)
\( - \frac{{3\pi }}{4}\)
\( - \frac{\pi }{2}\)
\( - \frac{\pi }{4}\)
0
\(\frac{\pi }{4}\)
\(\frac{\pi }{2}\)
\(\frac{{3\pi }}{4}\)
\(\pi \)
\(\sin x\)
\(0\)
\( - \frac{{\sqrt 2 }}{2}\)
\( - 1\)
\( - \frac{{\sqrt 2 }}{2}\)
0
\(\frac{{\sqrt 2 }}{2}\)
1
\(\frac{{\sqrt 2 }}{2}\)
0
c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)