Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để y<2 thì \(0,5x^2< 2\)
=>x2<4
=>-2<x<4
b: Để y>2 thì 0,5x2>4
=>x2>4
=>x>2 hoặc x<-2
c: Để -2<y<2 thì \(x\in\left(-2;4\right)\cap\left(\left(-\infty;-2\right)\cup\left(2;+\infty\right)\right)=\left(2;4\right)\)

a, Vì \(1-\sqrt{5}< 0\)nên hàm nghịch biến
b, \(x=1+\sqrt{5}x\)
\(\Leftrightarrow x-x\sqrt{5}=1\)
\(\Leftrightarrow x\left(1-\sqrt{5}\right)=1\)
\(\Leftrightarrow x=\frac{1}{1-\sqrt{5}}\)
Khi đó \(y=\left(1-\sqrt{5}\right).\frac{1}{1-\sqrt{5}}-1=1-1=0\)
b, \(y=-\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x-1=-\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x=1-\sqrt{5}\)
<=> x = 1

Bài giải:
a) Thế x = 4 và y = 11 vào y = 3x +b ta có: 11 = 3.4 + b ⇔ b = -1. Khi đó hàm số đã cho trở thành: y = 3x – 1. Đây là đường thẳng đi qua 2 điểm A(0;-1) và B(1/3; 0)
b) Đồ thị hàm số y = ax + 5 đi qua điểm A(-1; 3) nên: 3 = a(-1) + 5
<=> a = 2
Khi đó hàm số đã cho trở thành : y = 2x + 5. Đây là đường thẳng đi qua hai điểm A(0; 5) và B (−52;0)(−52;0)
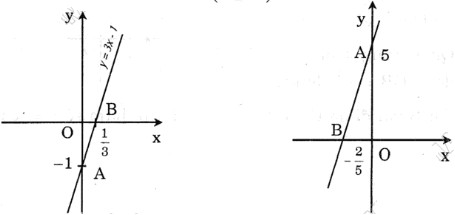

a) f(5) = 2; f(1) = 0; f(0) không tồn tại; f(-1) không tồn tại.
b) Để hàm số được xác định thì \(x-1\ge0\Leftrightarrow x\ge1\)
c) Gọi x0 là số bất kì thỏa mãn \(x\ge1\). Khi đó ta có:
\(h\left(x_0\right)=f\left[\left(x_0+1\right)-1\right]-f\left(x_0-1\right)=\sqrt{x_0}-\sqrt{x_0-1}\)
\(h\left(x_0\right)\left[f\left(x_0+1\right)+f\left(x_0\right)\right]=\left(\sqrt{x_0}-\sqrt{x_0-1}\right)\left(\sqrt{x_0}+\sqrt{x_0-1}\right)=x_0-\left(x_0-1\right)=1>0\)
Vì \(\sqrt{x_0}+\sqrt{x_0-1}>0\Rightarrow h\left(x_0\right)>0\)
Vậy thì với các giá trị \(x\ge1\) thì hàm số đồng biến.

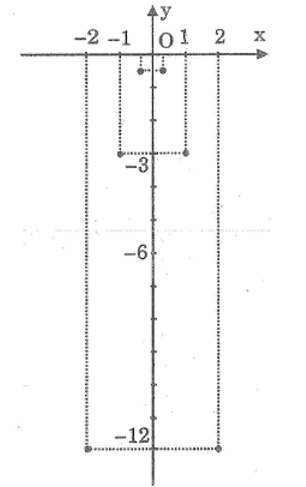
a: Khi x=-2 thì \(y=-3\cdot\left(-2\right)^2=-12\)
Khi x=-1 thì \(y=-3\cdot\left(-1\right)^2=-3\)
Khi x=-1/3 thì \(y=-3\cdot\dfrac{1}{9}=-\dfrac{1}{3}\)
Khi x=0 thì y=0
Khi x=1/3 thì \(y=-3\cdot\dfrac{1}{9}=-\dfrac{1}{3}\)
Khi x=1 thì y=-3
Khi x=2 thì y=-12
b:
a: f(5)=75/2
=>\(a\cdot5^2=\dfrac{75}{2}\)
=>\(a=\dfrac{75}{2}:25=\dfrac{3}{2}\)
Vậy: \(y=f\left(x\right)=\dfrac{3}{2}x^2\)
Khi x=-3 thì \(y=\dfrac{3}{2}\left(-3\right)^2=\dfrac{3}{2}\cdot9=\dfrac{27}{2}\)
b: y=15
=>\(\dfrac{3}{2}x^2=15\)
=>\(x^2=10\)
=>\(x=\pm\sqrt{10}\)