Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có:
\(\left\{{}\begin{matrix}1+1+a+b=0\\8+4+2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-2\\2a+b=-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-a=10\\a+b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-10\\b=8\end{matrix}\right.\)

Ta có :
\(\frac{1}{1^2}< \frac{1}{1.2};\frac{1}{2^2}< \frac{1}{2.3};...;\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Leftrightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}=1-\frac{1}{50}< 1< 2\)
Vậy A < 2
\(\frac{1}{1^2}=1\)
\(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
\(...\)
\(\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Rightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}\)
\(\Rightarrow A< 1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(\Rightarrow A< 1+1-\frac{1}{50}\)
\(\Rightarrow A< 2-\frac{1}{50}< 2\)
Vậy \(A< 2\)

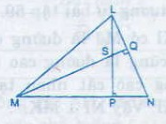
a) Chứng minh NS ⊥ LM
b) Khi =500, hãy tính góc MSP và góc PSQ
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có =500 nên
=400
∆MPS vuông tại Q có =400 nên
=500
Suy ra =1300(kề bù)




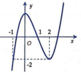
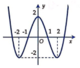
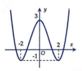

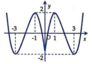

Đáp án C.
Tịnh tiến đồ thị hàm số y = f x sang trái 1 đơn vị.
Giữ nguyên phần đồ thị hàm số nằm bên phải trục tung. Xóa phần đồ thị hàm số nằm bên trái trục tung.
Lấy đối xứng phần đồ thị hàm số nằm bên phải trục tung qua trục tung.
Từ đây ta có đồ thị hàm số y = f x + 1 .