Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có :
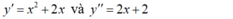
- Theo giả thiết x 0 là nghiệm của phương trình:
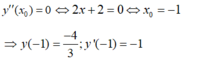
- Phương trình tiếp tuyến tại điểm 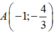 là:
là:
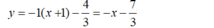
Chọn A.

Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm 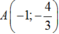 là: y = -1.(x + 1) - 7/3
là: y = -1.(x + 1) - 7/3
Hay  .
.

\(y'=-3x^2+6x+2m-1=-3x^2+6x-3+2m+2\)
\(y'=-3\left(x-1\right)^2+2m+2\le2m+2\)
\(\Rightarrow\) Hệ số góc lớn nhất của tiếp tuyến \(\left(C_m\right)\) là \(k=2m+2\)
Để tiếp tuyến song song với \(x-2y-4=0\Rightarrow y=\frac{1}{2}x-2\)
\(\Rightarrow k=\frac{1}{2}\Rightarrow2m+2=\frac{1}{2}\Rightarrow m=-\frac{3}{4}\)
Câu 2:
\(y'=\frac{\left(2x+\frac{1}{2\sqrt{x+1}}\right)x-\left(x^2-1+\sqrt{x+1}\right)}{x^2}\)
\(=\frac{4x^2\sqrt{x+1}+x-2x^2\sqrt{x+1}+2\sqrt{x+1}-2\left(x+1\right)}{2x^2\sqrt{x+1}}\)
\(=\frac{2x^2\sqrt{x+1}+2\sqrt{x+1}-x-2}{2x^2\sqrt{x+1}}\)
Hoặc làm thế này cũng được:
\(y=x-\frac{1}{x}+\frac{\sqrt{x+1}}{x}\)
\(\Rightarrow y'=1+\frac{1}{x^2}+\frac{\frac{x}{2\sqrt{x+1}}-\sqrt{x+1}}{x^2}\)
\(=1+\frac{1}{x^2}-\frac{x+2}{2x^2\sqrt{x+1}}\)
Sau đó quy đồng sẽ có kết quả giống bên trên

Câu 1:
Đặt \(f\left(x\right)=x^3+mx^2+\left(m-3\right)x-1\)
Ta có \(f\left(0\right)=-1\) ; \(f\left(-1\right)=1\)
\(\Rightarrow f\left(0\right).f\left(-1\right)< 0\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
Mặt khác \(\left\{{}\begin{matrix}f\left(0\right)=-1< 0\\\lim\limits_{x\rightarrow+\infty}=+\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;+\infty\right)\)
\(\left\{{}\begin{matrix}f\left(-1\right)=1>0\\\lim\limits_{x\rightarrow-\infty}=-\infty\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(-\infty;-1\right)\)
Vậy pt đã cho có 3 nghiệm phân biệt với mọi m
Câu 2:
\(f'\left(x\right)=x^2+2\left(m-1\right)x+m+1\)
Để \(f'\left(x\right)\ge0\) \(\forall x\) \(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m+1\right)\le0\)
\(\Leftrightarrow m^2-3m\le0\Leftrightarrow0\le m\le3\)
Câu 3:
Nhận thấy \(x=0\) không phải nghiệm
\(\Leftrightarrow2x^3+3x^2-2=-mx\)
\(\Leftrightarrow\frac{2x^3+3x^2-2}{x}=-m\)
Đặt \(f\left(x\right)=\frac{2x^3+3x^2-2}{x}\Rightarrow f'\left(x\right)=\frac{\left(6x^2+6x\right)x-\left(2x^3+3x^2-2\right)}{x^2}=\frac{4x^3+3x^2+2}{x^2}\)
\(f'\left(x\right)=\frac{4x^2\left(x+1\right)+2-x^2}{x^2}\Rightarrow f'\left(x\right)>0\) \(\forall x\in\left(-1;1\right)\)
\(\Rightarrow f\left(x\right)\) đồng biến trên \(\left(-1;1\right)\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=+\infty\) ; \(\lim\limits_{x\rightarrow0^+}f\left(x\right)=-\infty\)
\(\Rightarrow y=-m\) luôn cắt đồ thị \(y=f\left(x\right)\) hay phương trình đã cho luôn có ít nhất 1 nghiệm trong khoảng \(\left(-1;1\right)\) với mọi m

- Gọi d là tiếp tuyến của đồ thị hàm số đã cho qua A( 0, 2)
→ phương trình của d có dạng: y = k(x - 0) + 2 hay y = kx + 2
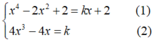
- Thay (2) vào (1) ta được :
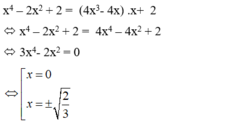
- Tương ứng với ba giá trị của x ta vừa tìm được, ta viết được 3 tiếp tuyến đi qua Ađến đồ thị (C).
Chọn B.

\(f'\left(x\right)=2x-2\)
a/ \(f'\left(1\right)=0\) ; \(f\left(1\right)=2\)
Phương trình tiếp tuyến: \(y=2\)
b/ \(4x-2y+5=0\Leftrightarrow y=2x+\frac{5}{2}\)
Tiếp tuyến song song d nên có hệ số góc bằng 2
\(\Rightarrow2x_0-2=2\Rightarrow x_0=2\)
\(f\left(2\right)=3\)
Pt tiếp tuyến: \(y=2\left(x-2\right)+3=0\Leftrightarrow y=2x-1\)
c/ \(x+4y=0\Rightarrow y=-\frac{1}{4}x\)
Tiếp tuyến vuông góc d \(\Rightarrow\) có hsg k thỏa mãn \(k.\left(-\frac{1}{4}\right)=-1\Rightarrow k=4\)
\(\Rightarrow2x_0-2=4\Rightarrow x_0=3\) ; \(f\left(3\right)=6\)
Pt tiếp tuyến: \(y=3\left(x-3\right)+6=3x-3\)
d/ Đường phân giác góc phần thứ thứ nhất có pt \(y=x\)
\(\Rightarrow\) Tiếp tuyến có hệ số góc -1
\(\Rightarrow2x_0-2=-1\Rightarrow x_0=\frac{1}{2}\) ; \(f\left(\frac{1}{2}\right)=\frac{9}{4}\)
Pt: \(y=-1\left(x-\frac{1}{2}\right)+\frac{9}{4}=-x+\frac{11}{4}\)

a) =
=
.
b) =
=
.
c) =
=
.
d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)
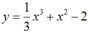
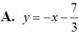
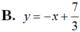
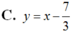
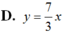


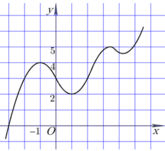
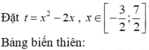
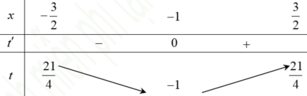




Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
- Phương trình tiếp tuyến tại điểm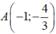 là:
là:
Chọn A.