Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Hoành độ giao điểm của đường thẳng y = m và (C) là nghiệm của phương trình :
\(x^4-2x^2=m\Leftrightarrow x^4-2x^2-m=0\) (*)
Đặt \(t=x^2,t\ge0\), phương trình (*) trở thành : \(t^2-2t-m=0\) (**)
Đường thẳng y = m và (C) cắt nhau tại 4 điểm phân biệt \(\Leftrightarrow\) phương trình (*) có 4 nghiệm phân biệt; \(\Leftrightarrow\) có 2 nghiệm phân biệt
\(t2 > t1 > 0\)\(\Leftrightarrow\begin{cases}\Delta'>0\\S>0\\P>0\end{cases}\) \(\Leftrightarrow\begin{cases}1+m>0\\2>0\\-m>0\end{cases}\) \(\Leftrightarrow\) \(-1 < m < 0\)
Khi đó phương trình (*) có 4 nghiệm là
\(x_1=-\sqrt{t_2};x_2=-\sqrt{t_1};x_3=\sqrt{t_1};x_4=\sqrt{t_2};\)
\(\Rightarrow x_1=-x_4;x_2=-x_3\)
Ta có \(y'=4x^3-4x\) do đó tổng các hệ số của tiếp tuyến tại cá điểm E, F, M, N là
\(k_1+k_2+k_3+k_4=\left(4x_1^3-4x_1\right)+\left(4x_2^3-4x_2\right)+\left(4x_3^3-4x_3\right)+\left(4x_4^3-4x_4\right)\)
\(=4\left(x_1^3+x^3_4\right)+4\left(x_2^3+x^3_3\right)-4\left(x_1+x_4\right)-4\left(x_2+x_3\right)=0\)
- Phương trình hoành độ giao điểm của d và (C) là
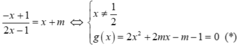
- Theo định lí Viet ta có x1+x2=-m; 
Giả sử A( x1; y1); B( x2; y2).
- Ta có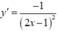 
nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là 
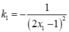và 
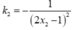.Vậy
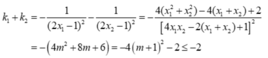
- Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng -2 khi m= -1.
Chọn A.
+ Phương trình hoành độ giao điểm của d và (C) là
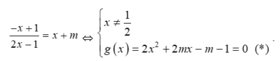
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có y ' = - 1 ( 2 x - 1 ) 2 , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
k 1 = - 1 ( 2 x 1 - 1 ) 2 ; k 2 = - 1 ( 2 x 2 - 1 ) 2
Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.
a. Tiếp tuyến của \(\left(C_m\right)\) tại điểm có hoành độ x = 1 có phương trình :
\(y=\left(m-2\right)\left(x-1\right)+3m-2=\left(m-2\right)x+3m\)
Yêu cầu của bài toán khi và chỉ khi \(\begin{cases}m-2=3\\2m\ne10\end{cases}\) vô nghiệm
Vậy không tồn tại m thỏa mãn yêu cầu bài toán
b. Ta có \(y'=3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+m-\frac{7}{3}=3\left(x-\frac{2}{3}\right)^2+m-\frac{7}{3}\)
Suy ra \(y'\ge m-\frac{7}{3}\)
Tiếp tuyến tại điểm có hoành độ \(x=\frac{2}{3}\) có hệ số góc nhỏ nhất và hệ số góc có giá trị \(k=m-\frac{7}{3}\)
Yêu cầu bài toán \(\Leftrightarrow k.2=-1\Leftrightarrow\left(m-\frac{7}{3}\right).2=-1\Leftrightarrow m=\frac{11}{6}\)
Phương trình có hoành độ giao điểm \(\frac{-x+m}{x+2}=-x+\frac{1}{2}\Leftrightarrow\begin{cases}x\ne-2\\2x^2+x+2m-2=0\left(1\right)\end{cases}\)
Đường thẳng (d) cắt \(\left(C_m\right)\) tại 2 điểm A, B <=> (1) có 2 nghiệm phân biệt \(x\ne-2\)
\(\Leftrightarrow\begin{cases}\Delta=1-8\left(2m-2\right)>0\\2\left(-2\right)^2+\left(-2\right)+2m-2\ne0\end{cases}\)\(\Leftrightarrow\begin{cases}17-16m>0\\m\ne-2\end{cases}\)\(\Leftrightarrow\begin{cases}m<\frac{17}{16}\\m\ne-2\end{cases}\)
\(A\left(x_1;-x_1+\frac{1}{2}\right);B\left(x_2;-x_2+\frac{1}{2}\right);\) trong đó x1, x2 là 2 nghiệm phân biệt của phương trình (1)
Theo Viet ta có \(\begin{cases}x_1+x_2=-\frac{1}{2}\\x_1x_2=m-1\end{cases}\)
\(AB=\sqrt{\left(x_2-x_1\right)^2+\left(x_1-x_2\right)^2}=\sqrt{2\left[\left(x_1+x_2\right)^2-4x_1x_2\right]}=\frac{\sqrt{2\left(17-16m\right)}}{2}\)
\(d\left(O,d\right)=\frac{1}{2\sqrt{2}};S_{\Delta OAB}=\frac{1}{2}AB.d\left(O,d\right)=\frac{1}{2}.\frac{1}{2\sqrt{2}}.\frac{\sqrt{2\left(17-16m\right)}}{2}=1\)
\(\Leftrightarrow m=\frac{-47}{16}\)
Vậy \(m=\frac{-47}{16}\)
Ta có \(\overrightarrow{n}=\left(2;1\right)\) là vecto pháp tuyến của đường thẳng d
\(y'=3x^2-2\left(m+2\right)x+m-1\Rightarrow y'\left(1\right)=3-2m-4+m-1=-m-2\)
Gọi \(\Delta\) là tiếp tuyến của đồ thị hàm số (1) tại điểm có hoành độ bằng 1. Suy ra phương trình của \(\Delta\) có dạng \(y=y'\left(1\right)\left(x-1\right)+y\left(1\right)\)
Do đó \(\overrightarrow{n}=\left(m+2;1\right)\) là vecto pháp tuyến của \(\Delta\)
Theo đề bài ta có : \(\left|\cos\left(\overrightarrow{n_1.}\overrightarrow{n_2}\right)\right|=\cos30^0\Rightarrow\frac{\left|\overrightarrow{n_1.}\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|}=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow\frac{\left|2\left(m+2\right)+1\right|}{\sqrt{5}\sqrt{\left(m+2\right)^2+1}}=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow m^2+20m+25=0\)
\(\Leftrightarrow m=-10\pm5\sqrt{3}\)
a) (C) có 2 tiệm cận xiên là x = -1 và y = x + 1
I là tâm đối xứng \(\Rightarrow I\left(-1;0\right)\) (I là giao của 2 tiệm cận)
Xét \(M\left(x_0;f\left(x_0\right)\right)\in\left(C\right)\). Tiếp tuyến \(\Delta\) tại M của (C) :
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=\frac{x_0^2+2x_0}{\left(x_0+1\right)^2}\left(x-x_0\right)+\frac{x^2_0+2x_0+2}{x_0+1}\)
Lời giải:
PT hoành độ giao điểm:
$\frac{-4x+12}{x+1}=2x+m$
$\Rightarrow -4x+12=(2x+m)(x+1)$
$\Leftrightarrow 2x^2+x(m+6)+m-12=0(*)$
Ta thấy:
\(2(-1)^2+(-1)(m+6)+m-12=-16\neq 0\)
$\Delta (*)=(m+6)^2-8(m-12)=m^2+4m+132=(m+2)^2+128>0$ với mọi $m$
$\Rightarrow (*)$ luôn có 2 nghiệm pb khác -1 với mọi $m$
Tức là $(d)$ cắt $(C)$ tại 2 điểm phân biệt với mọi $m$ (đpcm)
Câu 1:
\(f'\left(1\right)=g'\left(1\right)=k\)
\(h\left(x\right)=\frac{f\left(x\right)+2}{g\left(x\right)+1}\Rightarrow h'\left(x\right)=\frac{f'\left(x\right)\left[g\left(x\right)+1\right]-g'\left(x\right)\left[f\left(x\right)+2\right]}{\left[g\left(x\right)+1\right]^2}\)
\(\Rightarrow h'\left(1\right)=\frac{k\left(b+1\right)-k\left(a+2\right)}{\left(b+1\right)^2}=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\)
Mà \(h'\left(1\right)=k\Rightarrow k=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\Rightarrow\frac{b-a-1}{\left(b+1\right)^2}=1\)
\(\Leftrightarrow b-a-1=\left(b+1\right)^2\Rightarrow a=b-1-\left(b+1\right)^2\)
\(\Rightarrow a=-b^2-b-2\)
Câu 2:
\(y=f\left(x\right)=\frac{x+1}{x-2}\Rightarrow f'\left(x\right)=\frac{-3}{\left(x-2\right)^2}\)
Phương trình hoành độ giao điểm:
\(\frac{x+1}{x-2}=x+m\Leftrightarrow x+1=\left(x+m\right)\left(x-2\right)\)
\(\Leftrightarrow x^2+\left(m-3\right)x-2m-1=0\)
\(\Delta=\left(m-3\right)^2+4\left(2m+1\right)=\left(m+1\right)^2+12>0\)
\(\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt A và B có hoành độ giả sử là a và b
Theo Viet: \(\left\{{}\begin{matrix}a+b=3-m\\ab=-3m-1\end{matrix}\right.\) \(\Rightarrow3a+3b-ab=10\) (1)
Mặt khác do tiếp tuyến tại A và B song song
\(\Leftrightarrow\frac{-3}{\left(a-2\right)^2}=\frac{-3}{\left(b-2\right)^2}\Leftrightarrow\left[{}\begin{matrix}a-2=b-2\\a-2=2-b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4-b\end{matrix}\right.\)
TH1: \(a=b\) thay vào (1):
\(\Rightarrow-a^2+6a-10=0\left(vn\right)\)
TH2: \(a=4-b\)
\(\Rightarrow a+b=4\Rightarrow3-m=4\Rightarrow m=-1\)
Xét phương trình hoành độ giao điểm của đồ thị (C) và d :
\(\frac{2x+3}{x+2}=-2x+m\)\(\Leftrightarrow\begin{cases}x\ne-2\\2x^2+\left(6-m\right)x+3-2m=0\end{cases}\) (*)
Xét phương trình (*), ta có \(\Delta>0\), mọi \(m\in R\) và x=-2 không là nghiệm của (*) nên d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B với mọi m
Hệ số góc của tiếp tuyến tại A, tại B lần lượt là :
\(k_1=\frac{1}{\left(x_1+1\right)^2};k_2=\frac{1}{\left(x_2+1\right)^2}\) trong đó \(x_1,x_2\) là 2 nghiệm của phương trình (*)
Ta thấy :
\(k_1.k_2=\frac{1}{\left(x_1+1\right)^2.\left(x_2+1\right)^2}=\frac{1}{\left(x_1x_2+2x_1+2x_2+4\right)^2}=4\) (\(k_1>0;k_2>0\) )
Có \(P=\left(k_1\right)^{2014}+\left(k_2\right)^{2014}\ge2\sqrt{\left(k_1k_2\right)^{2014}}=2^{2015}\)
Do đó , Min \(P=2^{2015}\) đạt được khi và chỉ khi \(k_1=k_2\)
\(\Leftrightarrow\frac{1}{\left(x_1+2\right)^2}=\frac{1}{\left(x_2+2\right)^2}\Leftrightarrow\left(x_1+2\right)^2=\left(x_2+2\right)^2\)
Do \(x_1,x_2\) phân biệt nên ta có \(x_1+2=-x_2-2\)
\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow m=-2\)
Vậy giá trị cần tìm là \(m=-2\)