Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=\left(m-1\right)x^2-2mx+m+2\)(1)
+) Nếu \(m-1=0\Leftrightarrow m=1\)thì :
(1) \(\Leftrightarrow y=-2x+3\)là hàm số bậc nhất có hệ số góc \(-2< 0\Rightarrow\)hàm số nghịch biến trên \(R\)
=> Hàm số nghịch biến trên \(\left(-\infty;2\right)\)
Vậy khi \(m=1\)hàm số nghịch biến trên \(\left(-\infty;2\right)\)(2)
+) Nếu \(m-1\ne0\Leftrightarrow m\ne1\)thì (1) là hàm số bậc hai
(1) nghịch biến trên \(\left(-\infty;2\right)\)thì đồ thị h/s có bề lõm hướng lên trên
\(\Rightarrow\hept{\begin{cases}a=m-1>0\\-\frac{b}{2a}\ge2\end{cases}}\Leftrightarrow\hept{\begin{cases}m>1\\\frac{2m}{2\left(m-1\right)}\ge2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m>1\\m-2\left(m-1\right)\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>1\\m\le2\end{cases}}\)
\(\Rightarrow1< m\le2\)\(\Leftrightarrow\hept{\begin{cases}m>1\\m-2\left(m-1\right)\ge0\Leftrightarrow\hept{\begin{cases}m>1\\m\le2\end{cases}}\end{cases}}\)(3)
Từ (2) và (3) suy ra hàm số nghịch biến trên \(\left(-\infty;2\right)\)thì \(1\le m\le2\)

a) hệ số a=-2=>y luôn nghịch biến
b) a=1 >0 và -b/2a =-5 => (-5;+vc) y luôn đồng biến
c) hàm y có dạng y=a/(x+1)
a =-1 => y đồng biến (-vc;-1) nghich biến (-1;+vc
=>
(-3;-2) hàm y đồng biến
(2;3) hàm y đồng biến
a) Hàm số \(y=-2x+3\) có a = -2 < 0 nên hàm số nghịch biến trên R.
b. Xét tỉ số \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\left(x^2_1+10x_1+9\right)-\left(x^2_2+10x_2+9\right)}{x_1-x_2}\)
\(=\dfrac{\left(x_1-x_2\right)\left(x_1+x_2+10\right)}{x_1-x_2}=x_1+x_2+10\).
Với \(x_1;x_2\notin\left(-5;+\infty\right)\) thì \(x_1+x_2+10\ge0\) nên hàm số y đồng biến trên \(\left(-5;+\infty\right)\).
c) Xét tỉ số: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{-\dfrac{1}{x_1+1}+\dfrac{1}{x_2+1}}{x_1-x_2}=\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}\)
Trên \(\left(-3;-2\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}< 0\) nên hàm số y nghịch biến trên \(\left(-3;-2\right)\).
Trên \(\left(2;3\right)\) thì \(\dfrac{1}{\left(x_1+1\right)\left(x_2+1\right)}>0\) nên hàm số y đồng biến trên \(\left(2;3\right)\).

A. Đây là hàm số bậc nhất. a= -3 < 0 nên => Ngịch biến

Xét hai số thực \(a;b\) bất kì thỏa mãn \(a>b>1\)
\(f\left(a\right)-f\left(b\right)=a+\frac{1}{a}-\left(b+\frac{1}{b}\right)=a-b+\frac{1}{a}-\frac{1}{b}\)
\(=a-b-\frac{a-b}{ab}=\left(a-b\right)\left(1-\frac{1}{ab}\right)\)
Do \(a>b>1\Rightarrow\left\{{}\begin{matrix}a-b>0\\ab>1\Rightarrow\frac{1}{ab}< 1\Rightarrow1-\frac{1}{ab}>0\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)-f\left(b\right)>0\Rightarrow f\left(a\right)>f\left(b\right)\)
Vậy hàm đồng biến trên \(\left(1;+\infty\right)\)

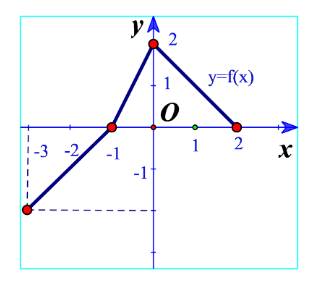
Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).

Do hàm số y = f(x) nghịch biến trên khoảng (a;b) nên
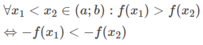
Vậy hàm số y = - f(x) đồng biến trên khoảng (a;b).
Hàm số \(y=-f\left(x\right)\) đồng biến trên khoảng \(\left(a;b\right)\)