



Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Xét hàm số:
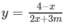
a) TXĐ: R \ {−3m/2}
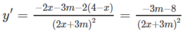
+) Nếu m < −8/3, y′ > 0 suy ra hàm số đồng biến trên các khoảng 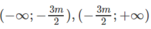
+) Nếu m > −8/3, y′ < 0 suy ra hàm số nghịch biến trên các khoảng
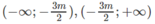
+) Nếu m = −8/3 thì y = −1/2 khi x ≠ 4
b) Ta có:
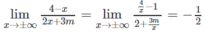
nên với mọi m, đường thẳng y = -1/2 là tiệm cận ngang và đi qua 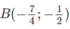
c) Số giao điểm của (Cm) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình:
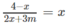
Ta có:
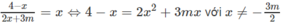
⇔ 2 x 2 + (3m + 1)x – 4 = 0 ⇔ 2 x 2 + (3m + 1) x – 4 = 0 với x ≠ −3m/2
+) Thay x = −3m/2 vào (*), ta có:
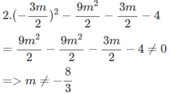
Như vậy, để x = −3m/2 không là nghiệm của phương trình (*) ta phải có m ≠ −8/3.
Ta có: Δ = ( 3 m + 1 ) 2 + 32 > 0, ∀ m. Từ đó suy ra với m ≠−8/3 đường thẳng y = x luôn cắt (Cm) tại hai điểm phân biệt.
d) Ta có:
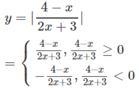
Trước hết, ta vẽ đồ thị (C) của hàm số
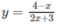
TXĐ: D = R \ {−3/2}.
Vì 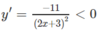
với mọi nên hàm số nghịch biến trên các khoảng
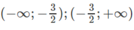
Bảng biến thiên:
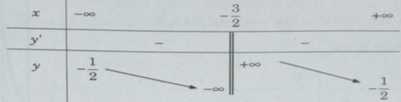
Tiệm cận đứng x = −3/2
Tiệm cận ngang y = −1/2
Đồ thị (C) đi qua các điểm (−2;−6),(−1;5),(0;4/3),(4;0)
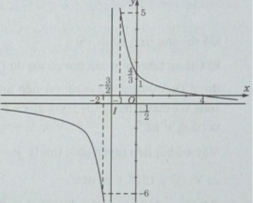
Để vẽ đồ thị (C’) của hàm số , ta giữ nguyên phần đồ thị (C) nằm phía trên trục hoành và lấy đối xứng phần đồ thị (C) nằm phía dưới trục hoành qua trục hoành.

a. Tiếp tuyến của \(\left(C_m\right)\) tại điểm có hoành độ x = 1 có phương trình :
\(y=\left(m-2\right)\left(x-1\right)+3m-2=\left(m-2\right)x+3m\)
Yêu cầu của bài toán khi và chỉ khi \(\begin{cases}m-2=3\\2m\ne10\end{cases}\) vô nghiệm
Vậy không tồn tại m thỏa mãn yêu cầu bài toán
b. Ta có \(y'=3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+m-\frac{7}{3}=3\left(x-\frac{2}{3}\right)^2+m-\frac{7}{3}\)
Suy ra \(y'\ge m-\frac{7}{3}\)
Tiếp tuyến tại điểm có hoành độ \(x=\frac{2}{3}\) có hệ số góc nhỏ nhất và hệ số góc có giá trị \(k=m-\frac{7}{3}\)
Yêu cầu bài toán \(\Leftrightarrow k.2=-1\Leftrightarrow\left(m-\frac{7}{3}\right).2=-1\Leftrightarrow m=\frac{11}{6}\)

Ta có \(y'=4x^3-16x\)
Vì \(x_0=1\Rightarrow y_0=m-6;y'\left(x_0\right)=-12\)
Phương trình tiếp tuyến d của \(\left(C_m\right)\) tại điểm có hoành độ \(x_0=1\) là :
\(y=-12\left(x-1\right)+m-6=-12x+m+6\)
Phương trình hoành độ giao điểm của \(\left(C_m\right)\) với d :
\(x^4-8x^2+m+1=-12x+m+6\Leftrightarrow x^4-8x^2+12-5=0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^2+2x-5\right)=0\Leftrightarrow x=1,x=-1\pm\sqrt{6}\)
Vậy d và \(\left(C_m\right)\) luôn cắt nhay tại 3 điểm
\(A\left(1;m-6\right);B\left(-1\pm\sqrt{6};m+18\ne\sqrt{6}\right)\)

Phương trình hoành độ giao điểm của \(\left(C_m\right)\) và đường thẳng y = -1 là :
\(x^4-\left(3m+2\right)x^2+3m=-1\Leftrightarrow\left(x^2-1\right)\left(x^2-3m-1\right)=0\)
Đường thẳng y = -1 cắt \(\left(C_m\right)\) tại 4 điểm phân biệt có hoành độ nhỏ hơn 2 khi và chỉ khi :
\(0 < 3m+1 < 4\) và \(3m+1\ne1\)
\(\Leftrightarrow\)\(-\frac{1}{3}< m\)< 1 và \(m\ne0\)



nên từ đồ thị (C) ta suy ra ngay đồ thị của hàm số :
\(y=\left|\dfrac{x^3}{6}+\dfrac{3x^2}{2}+\dfrac{5x}{2}\right|\) là hình 18


\(y=-x^4+2\left(m+1\right)x^2+m+1\left(C_m\right)\)
\(y'=-4x^2+4\left(m+1\right)x=-4x\left(x^2-m-1\right)\)
Xét \(y'=0\Leftrightarrow-4x\left(x^2-m-1\right)=0\) \(\Leftrightarrow\begin{cases}x=0\\x^2=m+1\left(1\right)\end{cases}\)
Hàm số có 3 điểm cực trị khi và chỉ khi phương trình \(y'=0\) có 3 nghiệm phân biệt \(\Leftrightarrow\) phương trình (1) có 2 nghiệm phân biệt khác 0
\(\Leftrightarrow m+1>0\Leftrightarrow m>-1\) (*)
Với điều kiện (*) phương trình y' = 0 có 3 nghiệm phân biệt \(x,x=\pm\sqrt{m+1}\) và có 3 điểm cực trị của đồ thị \(C_m\) là \(A\left(0;m+1\right);B\left(-\sqrt{m+1;}-\left(m+1\right)^2+m+1;\right);C\left(\sqrt{m+1};-\left(m+1\right)^2+m+1\right)\)
3 điểm cực trị tạo thành 1 tam giác đều :
\(\Leftrightarrow AB=AC=CB\Leftrightarrow AB^2=AC^2=CB^2\)
\(\Leftrightarrow\begin{cases}AB^2=AC^2\\AB^2=BC^2\end{cases}\)\(\Leftrightarrow\begin{cases}m+1+\left(m+1\right)^4=m+1+\left(m+1\right)^4\\m+1+\left(m+1\right)^4=4\left(m+1\right)\end{cases}\)
\(\Leftrightarrow m=\sqrt[3]{3}-1\)