Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tập xác định của hàm số f(x)và g(x) đều là ℝ .
Với x ∈ ℝ thì - x ∈ ℝ và ta có: f - x = - - x = - x = f x ;
g - x = - x + 1 - - x - 1 = x - 1 - x + 1 = - g x .
Vậy f(x)là hàm số chẵn, g(x) là hàm số lẻ. Đáp án là D.

Đáp án B
+ Hàm số f(x) và g(x) đều có tập xác định là D= R.
+ Xét hàm số y=f(x) : Với mọi ![]() và
và
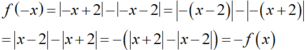
Nên y= f(x) là hàm số lẻ.
+ Xét hàm số y = g(x) :
Với mọi ![]() nên y = g(x) là hàm số chẵn.
nên y = g(x) là hàm số chẵn.
Chọn B.
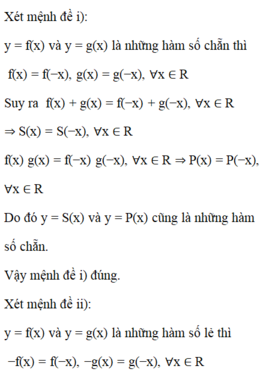
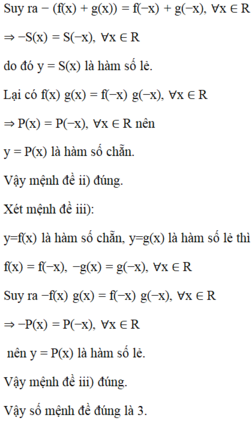
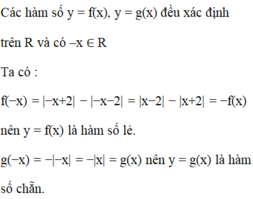
Lời giải:
TXĐ của cả $f(x),g(x): $D=\mathbb{R}$
Với $x\in D$ thì hiển nhiên $-x\in D$. Ta thấy:
\(f(x)=|x+2|+|x-2|=|-(x+2)|+|-(x-2)|\)
\(=|-x+2|+|-x-2|=f(-x)\)
Do đó $f(x)$ là hàm chẵn
\(-g(x)=-x^3-5x=[(-x)]^3+5(-x)=g(-x)\)
Do đó $g(x)$ là hàm lẻ.
Đáp án D
Lời giải:
TXĐ của cả $f(x),g(x): $D=\mathbb{R}$
Với $x\in D$ thì hiển nhiên $-x\in D$. Ta thấy:
\(f(x)=|x+2|+|x-2|=|-(x+2)|+|-(x-2)|\)
\(=|-x+2|+|-x-2|=f(-x)\)
Do đó $f(x)$ là hàm chẵn
\(-g(x)=-x^3-5x=[(-x)]^3+5(-x)=g(-x)\)
Do đó $g(x)$ là hàm lẻ.
Đáp án D