Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai đường thẳng cắt nhau khi 2m + 1 ≠ 2 hay m ≠ 0,5, k túy ý.
b) Hai đường thẳng song song với nhau khi 2m + 1 = 2 và 3k ≠ 2k - 3 hay khi m = 0,5 và k ≠ -3.
c) Hai đường thẳng trùng nhau khi 2m + 1 = 2 và 3k = 2k - 3 hay khi m = 0,5 và k = -3.
Bài giải:
a) Hai đường thẳng cắt nhau khi 2m + 1 ≠ 2 hay m ≠ 0,5, k túy ý.
b) Hai đường thẳng song song với nhau khi 2m + 1 = 2 và 3k ≠ 2k - 3 hay khi m = 0,5 và k ≠ -3.
c) Hai đường thẳng trùng nhau khi 2m + 1 = 2 và 3k = 2k - 3 hay khi m = 0,5 và k = -3

y = (k+1)x +3 (d)
và y = (3-2k)x + 1 (d’)
Các hàm số đã cho là hàm số bậc nhất khi:

a) Vì đã có 3 ≠ 1 nên (d) // (d’) khi và chỉ khi
k+1 = 3 – 2k
k = 2/3 (TMĐK (*))
Vậy với k = 2/3 thì đồ thị của hai hàm số là hai đường thẳng (d) và (d’) song song với nhau.
b) Hai đường thẳng (d) cắt (d’) khi và chỉ khi k+1 ≠ 3 – 2k
k ≠ 2/3
Vậy với k ≠ -1, k ≠3/2 và k ≠ 2/3 thì đồ thị của hai hàm số là hai đường thẳng (d) và (d’) cắt nhau.
c) Hai đường thẳng (d) và (d’) không thể trùng nhau vì có tung độ gốc khác nhau (do 3 ≠ 1).

Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.

Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
a) Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
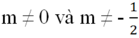
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
b) Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi:
m ≠ 2m + 1 => m ≠ -1.
Kết hợp với điều kiện trên, ta có:
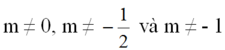

Lời giải:
a. Để hai đường thẳng cắt nhau thì:
$m\neq 2m+1$
$\Leftrightarrow m\neq 1$
b. Để hai đường thẳng song song với nhau thì:
$2m+1=m$
$\Leftrightarrow m=1$

Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
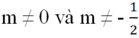
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.

2/ Để 2 đường thẳng này // thì
\(a-1=3-a\Leftrightarrow a=2\)
Phần còn lại không hiểu bạn muốn hỏi gì luôn. Chép câu hỏi gốc lên đi b
1/ Lên mạng tìm khái niệm nhé :)

2 hàm số bậc nhất \(y=mx+3,y=\left(2m+1\right)x-5\left(đk:m\ne0,m\ne-\dfrac{1}{2}\right)\)
a) Để 2 đường thẳng song song với nhau thì:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=2m+1\\3\ne-5\left(luôn.đúng\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m=-1\end{matrix}\right.\)
b) Để 2 đường thẳng cắt nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne2m+1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\ne-1\end{matrix}\right.\)
c) Để 2 đường thẳng vuông góc với nhau:
\(\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\m\left(2m+1\right)=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\\2m^2+m+1=0\left(VLý.do.2m^2+m+1=2\left(m+\dfrac{1}{4}\right)^2+\dfrac{7}{8}>0\right)\end{matrix}\right.\)
Vậy 2 đường thẳng này không vuông góc với nhau với mọi m
\(a,\Leftrightarrow\left\{{}\begin{matrix}m=2m+1\\-5\ne3\end{matrix}\right.\Leftrightarrow m=-1\\ b,\Leftrightarrow m\ne2m+1\Leftrightarrow m\ne-1\\ c,\Leftrightarrow m\left(2m+1\right)=-1\\ \Leftrightarrow2m^2+m+1=0\\ \Delta=1-8< 0\\ \Leftrightarrow m\in\varnothing\)
Vậy 2 đt không thể vuông góc nhau

a) Hàm số \(y=2x+3k\) có các hệ số \(a=2,b=3k\)
Hàm số \(y=\left(2m+1\right)x+2k-3\) có các hệ số \(a'=2m+1,b'=2k-3\)
Hai hàm số đã cho là hàm số bậc nhất nên \(2m+1\ne0\)
\(\Leftrightarrow m\ne-\frac{1}{2}\)
Hai đường thẳng song song với nhau khi \(a=a'\) và \(b\ne b'\) tức là:
\(2=2m+1\) và \(3k\ne2k-3\)
Kết hợp với điều kiện trên ta có: \(m=\frac{1}{2}.k\ne-3\)
b) Hai đường thẳng song song:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k\ne2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k\ne-3\end{cases}}\)
c) Hai đường thẳng trùng nhau:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k=2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k=-3\end{cases}}\)
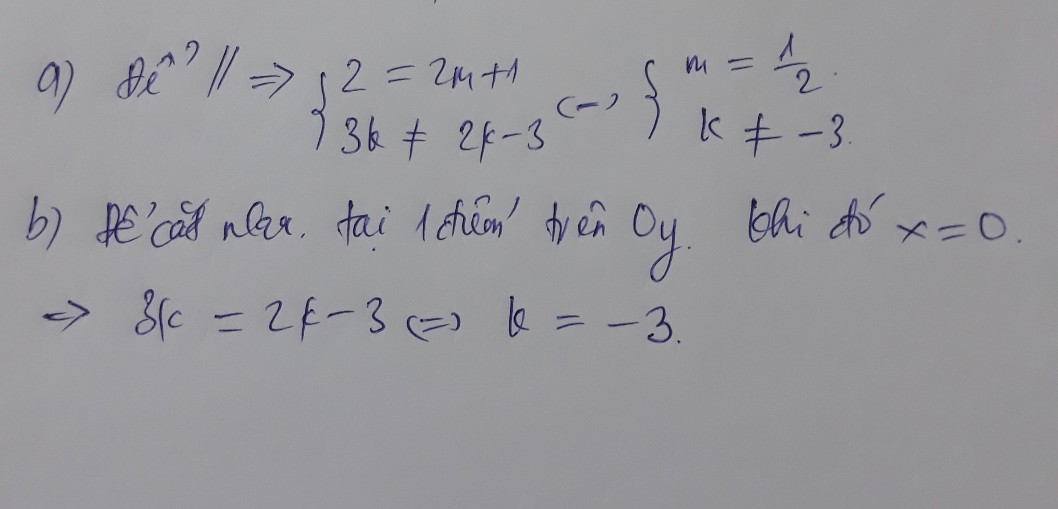
Cho hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5. Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau;
b) Hai đường thẳng cắt nhau.