Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ đồ thị:
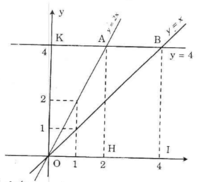
b) - Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4
=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)
- Tìm độ dài các cạnh của ΔOAB
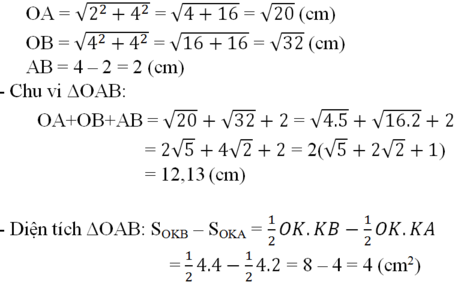
((*): muốn tìm tung độ hay hoành độ của một điểm khi đã biết trước hoành độ hay tung độ, ta thay chúng vào phương trình đồ thị hàm số để tìm đơn vị còn lại.)

Đường thẳng // với Ox và cắt Oy tại tung độ là 6 có phương trình: y = 6
Tọa độ A là nghiệm của hệ
\(\hept{\begin{cases}y=x\\y=6\end{cases}}\Leftrightarrow\hept{\begin{cases}x=6\\y=6\end{cases}}\)
=> A(6, 6)
Tọa độ B là nghiệm của hệ
\(\hept{\begin{cases}y=3x\\y=6\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=6\end{cases}}\)
=> B(2, 6)

a) 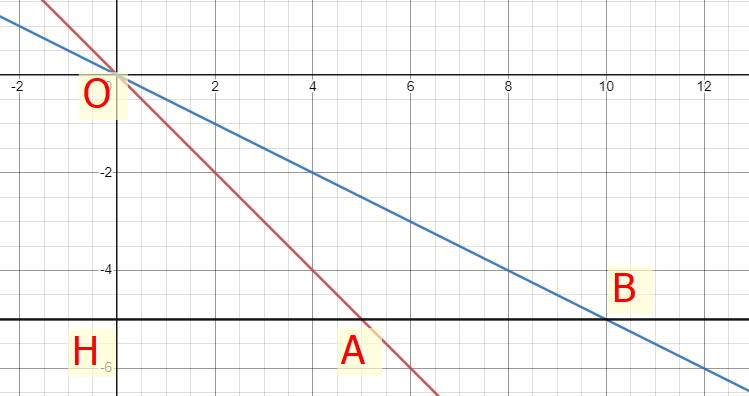
b) Ta có đường thẳng đi qua điểm H(0;-5) nên phương trình đường thẳng đi qua H là:
\(y=0x-5\Rightarrow y=-5\)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-x\) là:
\(-5=-x\)
\(\Rightarrow x=5\)
Tọa độ điểm A là (5;-5)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-\dfrac{1}{2}x\) là:
\(-5=-\dfrac{1}{2}x\)
\(\Rightarrow\dfrac{1}{2}x=5\)
\(\Rightarrow x=5:\dfrac{1}{2}\)
\(\Rightarrow x=10\)
Tọa độ điểm B là (10;-5)
c) Ta có: A(5;-5) và B(10;-5)
Độ dài đường thẳng AB là \(10-5=5\left(đvđd\right)\)
Có A(5;-5) ⇒ HA = 5 (đvđd)
Xét tam giác OHA vuông tại H áp dụng định lý Py-ta-go ta có:
\(OA^2=HA^2+OH^2\) (tọa độ điểm H(0;-5) nên OH = 5 đvđd)
\(\Rightarrow OA=\sqrt{5^2+5^2}=\sqrt{50}=5\sqrt{2}\left(đvđd\right)\)
Có B(10;-5) ⇒ HB = 10 (đvđd)
Xét tam giác OHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(OB^2=HB^2+OH^2\)
\(\Rightarrow OB=\sqrt{10^2+5^2}=\sqrt{125}=5\sqrt{5}\left(đvđd\right)\)
Chu vi: \(C_{OAB}=AB+OA+OB=5+5\sqrt{2}+5\sqrt{5}\approx23,25\left(đvđd\right)\)
Diện tích: \(S_{OAB}=\dfrac{1}{2}\cdot OH\cdot AB=\dfrac{1}{2}\cdot5\cdot5=12,5\left(đvdt\right)\)

Theo Cô si 4x+\frac{1}{4x}\ge24x+4x1≥2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1=1⇔x=41). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x+3+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x+3+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x+1+2014=x+1(2x−1)2+2014≥2014
Hơn nữa A=2014A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right.{x=412x−1=0 \Leftrightarrow x=\dfrac{1}{4}⇔x=41 .
Vậy GTNN = 2014
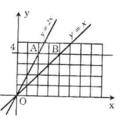
b. Đồ thị đt đề cho là y=6
PTGD 2 đt đầu bài với đt câu b là: \(\left\{{}\begin{matrix}2x=6\\x-1=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\rightarrow A\left(3;6\right)\\x=7\rightarrow B\left(7;6\right)\end{matrix}\right.\)