Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. a. Theo ht 4' trg đm //, ta có: Rtđ= (R1.R2)/(R1+R2)= (3.6)/(3+6)=2 ôm
b.Theo ĐL ôm, ta có: I= U/Rtđ=24/2=12 A
I1=U/R1=24/3=8 ôm
I2=U/R2=24/6=4 ôm
2. a. Theo ht 4' trg đm //, ta có: Rtđ=(R1.R2.R3)/(R1+R2+R3)= (6.12.4)/(6+12+4)=13,09 ôm
b. Áp dụng ĐL Ôm, ta có: U=I.R=3.13,09=39,27 V
c. Theo ĐL Ôm, ta có:
I1=U/R1=39,27/6=6.545 A
I2=U/R2=39,27/12=3,2725 A
I3=U/R3=39,27/4=9.8175 A

a. Điện trở tương đương của mạch là: R t đ = R 1 + R 2 = 40
Cường độ dòng điện qua mỗi điện trở là:
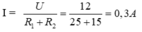
b. Đổi S = 0 , 06 m m 2 = 0 , 06 . 10 - 6 m 2
Công thức tính điện trở:
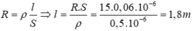
c. Cường độ dòng điện định mức của đèn:
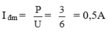
Vì đèn sáng bình thường nên hiệu điện thế giữa hai đầu R 1 là 6V
Vậy hiệu điện thế hai đầu biến trở là: U b = U - U đ = 12 - 6 = 6 V
ường điện dòng điện chạy qua R 1 là: I 1 = 6 / 25 = 0 , 24 A
Cường điện dòng điện chạy qua biến trở là: I b = I 1 + I đ m = 0 , 74 A
Vậy điện trở biến trở khi đó là:
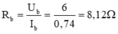

Điện trở tương đương của đoạn mạch là:
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{30.60}{30+60}=20\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=30V\)
Cường độ dòng điện chạy qua mạch chính và mỗi mạch rẽ:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{30}{20}=1,5\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{30}{30}=1\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{30}{60}=0,5\left(A\right)\end{matrix}\right.\)
Điện trở tương đương lúc này là:
\(R_{tđ}=R_{12}+R_3=20+40=60\left(\Omega\right)\)
Do mắc nối tiếp nên \(I=I_{12}=I_3=1,5\left(A\right)\)
Nhiệt năng đoạn mạch tiêu thụ trong 30ph:
\(A=P.t=I^2.R.t=1,5^2.60.30.60=243000\left(J\right)\)
Nhiệt lượng tỏa ra của R3 trong 30ph:
\(Q_{tỏa_3}=A_3=I_3^2.R_3.t=1,5^2.40.30.60=162000\left(J\right)\)

a. \(R=\dfrac{R1\cdot R2}{R1+R2}=\dfrac{30\cdot20}{30+20}=12\Omega\)
b. \(U=U1=U2=IR=2\cdot12=24V\left(R1//R2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}I1=U1:R1=24:30=0,8A\\I2=U2:R2=24:20=1,2A\end{matrix}\right.\)
c. \(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p\cdot l}{R}=\dfrac{0,5\cdot10^{-6} \cdot2}{30}=3,\left(3\right)\cdot10^{-8}\Omega m\)

a. Điên trở tương đương của đoạn mạch này là :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.12}{60+12}=10\Omega\)
b. CĐDĐ qua mạch chính là :
\(I=\dfrac{U}{R}=\dfrac{2,4}{10}=0,24A\)
Vì \(R_1\)//\(R_2\) nên :
\(U=U_1=U_2=2,4V\)
CĐDĐ qua các đoạn mạch rẽ là :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{2,4}{60}=0,04A\)
\(\Rightarrow I_2=0,24-0,04=0,2A\)
c. Vì điện trở \(R_3\) nt ( \(R_1\)//\(R_2\)) nên điện trở tương đương toàn mạch là :
\(R_{123}=R_{12}+R_3=10+16=26\Omega\)
\(\Rightarrow\) CĐDĐ qua mạch chính là :
\(I=\dfrac{U}{R_{123}}=\dfrac{2,4}{26}\approx0,1A\)
Vậy : a. Điện trở tương đương của đoạn mạch \(R_1\)//\(R_2\) là \(10\Omega\)
b. I = 0,24A ; \(I_1=0,04A\) ; \(I_2=0,2A\)
c. \(I_{123}\) = 0,1A

a) \(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{10.15}{10+15}=6\left(\Omega\right)\)
b) \(U=U_1=U_2=12V\)
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{12}{10}=1,2\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{15}=0,8\left(A\right)\end{matrix}\right.\)
\(P_1=I_1^2.R_2=1,2^2.10=14,4\left(W\right)\)
\(P_2=I_2^2.R_2=0,8^2.15=9,6\left(W\right)\)

Giúp e với ạ