Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{COB}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=BC
b: Xét ΔABD và ΔCDB có
AB=CD
\(\widehat{ABD}=\widehat{CDB}\)
DB chung
Do đó: ΔABD=ΔCDB
Suy ra: \(\widehat{HAB}=\widehat{HCD}\)
Xét ΔHAB và ΔHCD có
\(\widehat{HAB}=\widehat{HCD}\)
AB=CD
\(\widehat{HBA}=\widehat{HDC}\)
Do đó: ΔHAB=ΔHCD
c: Xét ΔAOH và ΔCOH có
OA=OC
OH chung
HA=HC
Do đó: ΔAOH=ΔCOH
Suy ra: \(\widehat{AOH}=\widehat{COH}\)

HÌnh bạn tự vẽ (vẽ góc nhọn)
a) Xét \(\Delta COB\)và \(\Delta AOD\)ta có:
OB=OA
Góc xOy chung
OC=OD
\(\Rightarrow\Delta COB=\Delta AOD\left(c-g-c\right)\)
\(\Rightarrow BC=AD\)(cặp cạnh tương ứng)
b) Bạn ghi lại, đề bài sai nên phần c chưa làm đc!

Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
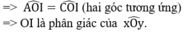

a)Xét tam giác AOD VÀ COB có AO=OC ,OB=OD ,chung góc O=> tam giác AOD =tam giác COB(cgc)=>AD=BC
b) Ta có OA=OC,OB=OC=> AB=CD.
Tam giác AOD=tg COB=> góc OAD =góc BCO góc
Và ADO=gócCBO(2 góc tương ứng).
Mà góc ABI + góc CBO=180 độ(kề bù)
góc CDI+góc ADO=180 độ (kề bù)
=> Góc CBO=ADO
Xét tg ABI và tg CDI có AB= CD(cm trên),gics CBO= góc ADO,góc OAC= BCO=> tg ABI=th CDI => AI=CI,BI=Di

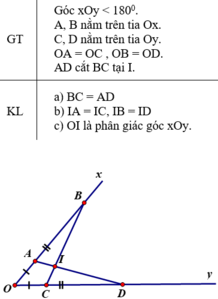
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)

a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
ˆxOyxOy^ là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
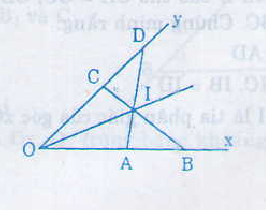
b) ∆AOD = ∆COB => ˆAOD=ˆOCBAOD^=OCB^
=> ˆBAI=ˆDCIBAI^=DCI^ (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
ˆDCI=ˆABIDCI^=ABI^ ( ∆AOD = ∆COB)
ˆBAI=ˆDCIBAI^=DCI^ (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> ˆCOI=ˆAOICOI^=AOI^
=> OI là phân giác của ˆxOy
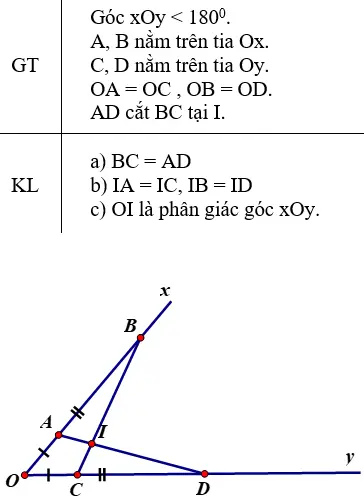
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
b) – ΔAOD = ΔCOB
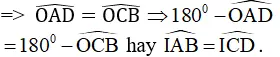
Lại có: OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
– Xét ΔDIC và ΔBIA có:
CD = AB (chứng minh trên)
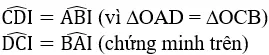
⇒ ΔDIC = ΔBIA (g.c.g)
⇒ IC = IA và ID = IB (các cặp cạnh tương ứng)
c) Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)
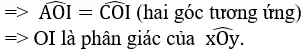

a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
ˆxOyxOy^ là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC

b) ∆AOD = ∆COB => ˆAOD=ˆOCBAOD^=OCB^
=> ˆBAI=ˆDCIBAI^=DCI^ (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
ˆDCI=ˆABIDCI^=ABI^ ( ∆AOD = ∆COB)
ˆBAI=ˆDCIBAI^=DCI^ (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> ˆCOI=ˆAOICOI^=AOI^
=> OI là phân giác của ˆxOy
Hướng dẫn:
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
ˆxOyxOy^ là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC

b) ∆AOD = ∆COB => ˆAOD=ˆOCBAOD^=OCB^
=> ˆBAI=ˆDCIBAI^=DCI^ (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
ˆDCI=ˆABIDCI^=ABI^ ( ∆AOD = ∆COB)
ˆBAI=ˆDCIBAI^=DCI^ (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> ˆCOI=ˆAOICOI^=AOI^
=> OI là phân giác của ˆxOy