Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha!
Tam giác AOC có: AO = CO nên tam giác AOC cân tại O
\(\Rightarrow OAC=\frac{180-O}{2}\)
Tam giác BOD có OB = OD nên tam giác BOD cân tại O
\(\Rightarrow OBD=\frac{180-O}{2}\)
\(\Rightarrow OAC=OBD\)Mà hai góc này ở vị trí đồng vị nên AC song song với BD.

a/xét OBC và ODA:
-góc O chung
-OD=OB(gt)
-OA=OC(gt) => OBC=ODA =>AD=BC
b/ từ a/ =>gADO = gOBC và gOAD = gOCB =>gBAD=gBCD (bù với 2 g = nhau)
OA=OC và OD=OB => AB=CD
-xét tam giác EAB và ECD:
AB=CD
gBAD=gBCD
gADO=gOBC =>dpcm
c/b/=>ED=EB
xét OBE và ODE: ED=EB
gB=gD
OB=OD =>2 tg = nhau
=>gBOE=gDOE =>OE là p/g
d/gọi M:trung điểm BD
xét tam giác OBM và ODM: OM chung
gBOE=gDOE
OB=OD => 2 tam giác = nhau
=> BM=DM và gBMO=gDMO mà tổng = 180 =>....
e/cm tương tự d/=> OE là trung trực AC
=>gOAC = gOBD (phụ với gBOE) => AC//BD

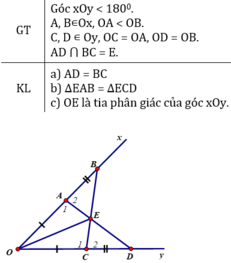
ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

Do ΔOAD = ΔOCB (chứng minh trên)
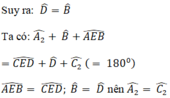
OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
Xét ΔAEB và ΔCED có:
∠B = ∠D
AB = CD
∠A2 = ∠C2
⇒ΔAEB = ΔCED (g.c.g)

ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒  (hai góc tương ứng)
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.

a) ∆OAD và ∆OCB có: OA= OC(gt)
=
(=
)
OD=OB(gt)
Nên ∆OAD=∆OCB(c.g.c)
suy ra AD=BC.
b) ∆OAD=∆OCB(cmt)
Suy ra: =
=
=>
=
Do đó ∆AOE = ∆OCE(c .c.c)
suy ra: =
vậy OE là tia phân giác của xOy.
b) ∆AEB= ∆CED(câu b) => EA=EC.
∆OAE và ∆OCE có: OA=OC(gt)
EA=EC(cmt)
OE là cạnh chung.
Nên ∆OAE=∆(OCE)(c .c.c)
suy ra: =
vậy OE là tia phân giác của góc xOy.
Xét △AOD và △COB có:
AO=CO (gt)
∠O là góc chung
OD=OB(gt)
nên △AOD = △COB (c-g-c)
do đó AD = CB
Ta có: OA+AB=OB
OC+CD=OD
mà OA = OB (gt)
OC = OD (gt)
nên AB=CD
Xét △BCD và △DAB có:
CD=AB (gt)
BD là cạnh chung
AD = CB (cmt)
nên △BCD = △DAB
do đó: ∠DBC=∠BDA
suy ra:∠DBC=(180o - ∠BED):2
Chứng minh tương tự ta được: △ACD = △CAB
do đó: ∠CAD=∠ACB
suy ra: ∠ACB=(180o - ∠CEA):2
Ta lại có: ∠DBC=(180o - ∠BED):2 (cmt)
mà ∠BED = ∠CEA (đối đỉnh)
nên ∠ACB=∠DBC
mà hai góc này ở vị trí so le trong
vậy AC song song với BD