Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì 0 < α < π/2 nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.

a) Do \(\pi< \alpha< \dfrac{3\pi}{2}\) nên \(sin\alpha< 0;cot\alpha>0;tan\alpha>0\).
Vì vậy: \(sin\alpha=-\sqrt{1-cos^2\alpha}=\dfrac{-\sqrt{15}}{4}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{15}}{4}:\dfrac{-1}{4}=\sqrt{15}\).
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{1}{\sqrt{15}}\).
b) Do \(\dfrac{\pi}{2}< \alpha< \pi\) nên \(cos\alpha< 0;tan\alpha< 0;cot\alpha< 0\).
\(cos\alpha=-\sqrt{1-sin^2\alpha}=-\dfrac{\sqrt{5}}{3}\);
\(tan\alpha=\dfrac{2}{3}:\dfrac{-\sqrt{5}}{3}=\dfrac{-2}{\sqrt{5}}\); \(cot\alpha=1:tan\alpha=\dfrac{-\sqrt{5}}{2}\).

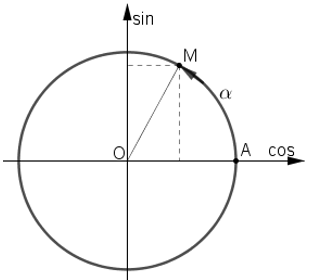
Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy
=> = cosα;
=
= sinα;
Trong tam giác vuông MPO:
MP2+ PO2 = OM2 => cos2 α + sin2 α = 1

a)\(\sin^2\alpha+\cos^2\alpha=1\Rightarrow\sin^2\alpha=1-\cos^2\alpha\)
\(\Rightarrow1-2^2=-3\) \(\Rightarrow\cos=-\sqrt{3}\left(0< \alpha< \dfrac{\pi}{2}\right)\)
b) \(\tan\alpha\times\cot\alpha=1\Rightarrow\tan\alpha=\dfrac{1}{\cot\alpha}\Rightarrow\tan=\dfrac{1}{4}\)
a)Do \(0< \alpha< \dfrac{\pi}{2}\) nên các giá trị lượng giác của \(\alpha\) đều dương.
\(cos\alpha=2sin\alpha\)(1)
Nếu \(sin\alpha=0\Rightarrow cos\alpha\) (vô lý).
Vì vậy \(sin\alpha\ne0\) . Từ (1) \(\Rightarrow\dfrac{cos\alpha}{sin\alpha}=2\)\(\Leftrightarrow cot\alpha=2\).
Suy ra: \(tan\alpha=\dfrac{1}{2}\).
\(sin\alpha=\sqrt{\dfrac{1}{1+cot^2\alpha}}=\dfrac{1}{\sqrt{3}}\).
\(cos\alpha=\sqrt{1-sin^2\alpha}=\sqrt{\dfrac{2}{3}}\).

a) Do 0 < α < nên sinα > 0, tanα > 0, cotα > 0
sinα =
cotα = ; tanα =
b) π < α < nên sinα < 0, cosα < 0, tanα > 0, cotα > 0
cosα = -√(1 - sin2 α) = -√(1 - 0,49) = -√0,51 ≈ -0,7141
tanα ≈ 0,9802; cotα ≈ 1,0202.
c) < α < π nên sinα > 0, cosα < 0, tanα < 0, cotα < 0
cosα = ≈ -0,4229.
sinα =
cotα = -
d) Vì < α < 2π nên sinα < 0, cosα > 0, tanα < 0, cotα < 0
Ta có: tanα =
cosα =

cotα = \(\frac{1}{3}\) \(\Leftrightarrow\frac{cos\alpha}{\sin\alpha}=\frac{1}{3}\Leftrightarrow\sin\alpha=3\cos\alpha\)
cotα =\(\frac{1}{\tan\alpha}=\frac{1}{3}\Rightarrow\tan\alpha=3\)
T = \(\frac{2016}{\sin^2\alpha-\sin\alpha\cos\alpha-\cos^2\alpha}=\frac{2016}{9\cos^2\alpha-3\cos^2\alpha-\cos^2\alpha}\) \(=\frac{2016}{5\cos^2\alpha}=\frac{2016}{5}\times\frac{1}{\cos^2\alpha}=\frac{2016}{5}\times\left(1+\tan^2\alpha\right)\) \(=\frac{2016}{5}\left(1+9\right)=4032\)

b) Do \(0< \alpha< \dfrac{\pi}{2}\) nên các giá trị lượng giác của \(\alpha\) đều dương.
Vì vậy:
\(cos\alpha=\sqrt{1-0,6^2}=\dfrac{4}{5}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=0,6:\dfrac{4}{5}=0,75;cot\alpha=1:tan\alpha=\dfrac{4}{3}\).
Do \(\dfrac{\pi}{2}< \alpha< \pi\) nên \(sin\alpha>0;tan\alpha< 0;cot\alpha< 0\).
\(sin\alpha=\sqrt{1-cos^2\alpha}=\dfrac{\sqrt{51}}{10}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\sqrt{51}}{10}:\left(-0,7\right)=-\dfrac{\sqrt{51}}{7}\).
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{-7}{\sqrt{51}}\).

D
D