
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BN
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
21 tháng 7 2017
Lời giải:
Áp dụng định lý về dấu của tam thức bậc 2.
a)
Để hàm \(f(x)=4x^2-(m+2)x+2m-3>0\forall x\in\mathbb{R}\)
\(\Leftrightarrow \Delta=(m+2)^2-16(2m-3)<0\)
\(\Leftrightarrow m^2-28m+52=(m-2)(m-26)<0\)
\(\Leftrightarrow 2< m<26\)
b)
Nếu \(m=-1\rightarrow f(x)=-6x\) không thể âm với mọi $x$
Nếu \(m\neq -1\):
Để \(f(x)=(m+1)x^2+2(2m-1)x-m-1<0\forall x\in\mathbb{R}\) thì cần hai đk sau:
1. \(m+1<0\leftrightarrow m<-1\)
2. \(\Delta'=(2m-1)^2+(m+1)^2<0\) (hiển nhiên vô lý)
Vậy không tồn tại $m$ thỏa mãn.
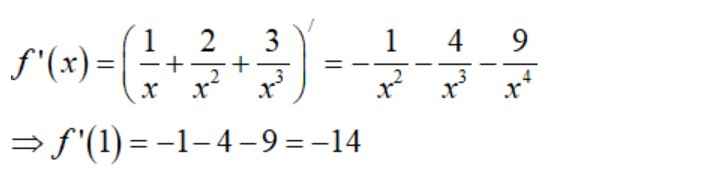
\(f\left(x\right)=x-\dfrac{1}{x}\Rightarrow f'\left(x\right)=1+\dfrac{1}{x^2}\); \(f''\left(x\right)=-\dfrac{2}{x^3}=\dfrac{\left(-1\right)^{2-1}.2!}{x^{2+1}}\) ;
\(f^{\left(3\right)}\left(x\right)=\dfrac{6}{x^4}=\dfrac{\left(-1\right)^{3-1}.3!}{x^{3+1}}\)
\(\Rightarrow f^{\left(n\right)}\left(x\right)=\dfrac{\left(-1\right)^{n-1}.n!}{x^{n+1}}\)