Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
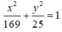
có a 2 = 169 ⇒ a = 13, b 2 = 25 ⇒ b = 5
c 2 = a 2 - b 2 = 169 - 25 = 144 ⇒ c = 12
Với điểm M bất kì thuộc elip ta có: MF1 + MF2 = 2a = 2.13 = 26
F1F2 = 2c = 2.12 = 24
Chu vi tam giác MF1F2: C = MF1 + MF2 + F1F2 = 26 + 24 = 50

Bạn xem lại đề ạ!
Nếu bạn đã chứng minh được D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ
Thì dễ dàng suy ra được: \(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\); \(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\); \(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
( Vì chúng ta có tính chất: Nếu I là trung điểm đoạn thẳng AB thì mọi điểm M ta có: \(2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}\))

\(F_1\left(-2\sqrt{2};0\right);F_2\left(2\sqrt{2};0\right)\)
Gọi \(M\left(x;y\right)\Rightarrow\frac{x^2}{9}+\frac{y^2}{1}=1\) (1) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{F_1M}=\left(x+2\sqrt{2};y\right)\\\overrightarrow{F_2M}=\left(x-2\sqrt{2};y\right)\end{matrix}\right.\)
Do \(\widehat{F_1MF_2}=90^0\Rightarrow F_1M\perp F_2M\Rightarrow\overrightarrow{F_1M}.\overrightarrow{F_2M}=0\)
\(\Rightarrow\left(x-2\sqrt{2}\right)\left(x+2\sqrt{2}\right)+y^2=0\Rightarrow x^2+y^2=8\) (2)
Từ (1) và (2) có hệ: \(\left\{{}\begin{matrix}\frac{1}{9}x^2+y^2=1\\x^2+y^2=8\end{matrix}\right.\) \(\Rightarrow x^2=\frac{63}{8}\Rightarrow x=\frac{3\sqrt{14}}{4}\)
Câu 2:
\(F_1F_2=24=2c\Rightarrow c=12\)
\(2a=26\Rightarrow a=13\)
\(\Rightarrow b^2=a^2-c^2=13^2-12^2=25\Rightarrow b=5\)
Vậy xưởng cao 5m

a) (E) có tiêu điểm \({F_1}\left( { - \sqrt 3 ;0} \right)\) nên \(c = \sqrt 3\).
Phương trình chính tăc của (E) có dạng
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có: \(M\left( {1;{{\sqrt 3 } \over 2}} \right) \in (E)\)
\(\Rightarrow {1 \over {{a^2}}} + {3 \over {4{b^2}}} = 1\ (1)\)
Và \({a^2} = {b^2} + {c^2} = {b^2} + 3\)
Thay vào (1) ta được :
\(\eqalign{ & {1 \over {{b^2} + 3}} + {3 \over {4{b^2}}} = 1 \cr & \Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^2}(b + 3) \cr}\)
\(\Leftrightarrow 4{b^4} + 5{b^2} - 9 = 0 \Leftrightarrow {b^2} = 1\)
Suy ra \({a^2} = 4\)
Ta có a = 2 ; b = 1.
Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0)
(0 ; -1) và (0 ; 1).
b) Phương trình chính tắc của (E) là :
\({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)
c) (E) có tiêu điểm thứ hai là điểm \(\left( {\sqrt 3 ;0} \right)\). Đường thẳng \(\Delta\) đi qua điểm\(\left( {\sqrt 3 ;0} \right)\) và vuông góc với Ox có phương trình \(x = \sqrt 3\).
Phương trình tung độ giao điểm của \(\Delta\) và \((E)\) là :
\({3 \over 4} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = \pm {1 \over 2}\)
Suy ra tọa độ của C và D là :
\(C\left( {\sqrt 3 ; - {1 \over 2}} \right)\) và \(\left( {\sqrt 3 ;{1 \over 2}} \right)\)
Vậy CD = 1.


Từ phương trình chính tắc của (E) ta có các thông tin về các bán trục và bán tiêu cự a = 13, b = 5, c = 12.