Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔACB vuông tại C
ΔOCD cân tại O
mà OI là đường cao
nên I là trung điểm của CD
=>IC=ID=CD/2=8cm
Xét ΔCAB vuông tại C cso CI là đường cao
nên CI^2=IA*IB
=>8^2=6*IB
=>IB=64/6=32/3(cm)
AB=IB+IA=32/3+6=50/3(cm)
=>R=50/3:2=25/3(cm)

a: kẻ OH\(\perp\)CD tại H
Ta có: OH\(\perp\)CD
AP\(\perp\)CD
QB\(\perp\)CD
Do đó: OH//AP//QB
Xét hình thang ABQP(AP//QB) có
O là trung điểm của AB
OH//AP//BQ
Do đó: H là trung điểm của PQ
=>HP=HQ
Ta có: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
=>HC=HD
Ta có: HC+CP=HP
HD+DQ=HQ
mà HP=HQ và HC=HD
nên CP=DQ
b: Ta có: ΔOCD vuông tại O
=>\(OC^2+OD^2=CD^2\)
=>\(CD^2=R^2+R^2=2R^2\)
=>\(CD=R\sqrt{2}\)
Xét ΔOAC có OA=OC=AC=R
nên ΔOAC đều
=>\(\widehat{CAO}=60^0\)
=>\(\widehat{CAB}=60^0\)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C có \(sinCAB=\dfrac{CB}{AB}\)
=>\(\dfrac{CB}{2R}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(CB=R\sqrt{3}\)


\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)

b.
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)
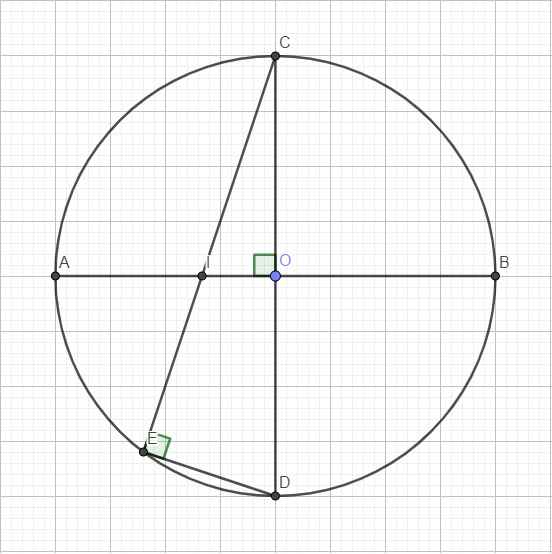
Đề thiếu. Bạn coi lại đề.